题目内容
一元一次方程
+
+
+…+
=1025的解是( )
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 3×4 |
| x |
| 1025×1026 |
| A、1024 | B、1025 |
| C、1026 | D、1027 |
考点:解一元一次方程
专题:
分析:提取x,根据
+
+…+
=1-
+
-
+…-
+
-
即可化简该式,即可解题.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 1025×1026 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 1025 |
| 1 |
| 1025 |
| 1 |
| 1026 |
解答:解:原式提取x,得x(
+
+…+
)=1025,
∴x(1-
+
-
+…-
+
-
)=1025,
解得:x=1026.
故选C.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 1025×1026 |
∴x(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 1025 |
| 1 |
| 1025 |
| 1 |
| 1026 |
解得:x=1026.
故选C.
点评:本题考查了一元一次方程的解,本题中根据
+
+…+
=1-
+
-
+…-
+
-
化简原式是解题的关键.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 1025×1026 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 1025 |
| 1 |
| 1025 |
| 1 |
| 1026 |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
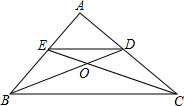 如图,在Rt△ABC中,∠A=90°,角平分线BD、CE交于O,OC=7,S四边形BEDC=56,求BC长.
如图,在Rt△ABC中,∠A=90°,角平分线BD、CE交于O,OC=7,S四边形BEDC=56,求BC长.