题目内容
在△ABC和△A′B′C′中,如果∠A=56°,∠B=28°,∠A′=56°,∠C′=28°,那么这两个三角形能否相似的结论是 ,理由是 .
考点:相似三角形的判定
专题:
分析:由已知条件易得∠A=∠A′,∠B=∠C′,则根据有两组角对应相等的两个三角形相似可判断两三角形相似.
解答:解:∵∠A=56°,∠B=28°,∠A′=56°,∠C′=28°,
∴∠A=∠A′,∠B=∠C′,
∴△ABC∽△A′C′B′.
故答案为△ABC∽△A′C′B′;有两组角对应相等的两个三角形相似.
∴∠A=∠A′,∠B=∠C′,
∴△ABC∽△A′C′B′.
故答案为△ABC∽△A′C′B′;有两组角对应相等的两个三角形相似.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
一元一次方程
+
+
+…+
=1025的解是( )
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 3×4 |
| x |
| 1025×1026 |
| A、1024 | B、1025 |
| C、1026 | D、1027 |
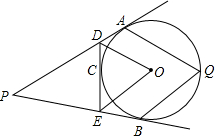 如图,从⊙O外一定点P作⊙O的两条切线,若C为
如图,从⊙O外一定点P作⊙O的两条切线,若C为
 如图,AB是⊙O的直径,半径OC⊥AB,点D、E分别在OA、OC上,且OD=OE,直线BE交⊙O于点F,判断直线AF、DC的位置关系,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,点D、E分别在OA、OC上,且OD=OE,直线BE交⊙O于点F,判断直线AF、DC的位置关系,并说明理由.