题目内容
已知关于x的方程a(3x-2)+b(2x-3)=8x-7.
(1)若b=1,a≠2时,求方程的解;
(2)当a,b满足什么条件时,方程有无数个解?
(1)若b=1,a≠2时,求方程的解;
(2)当a,b满足什么条件时,方程有无数个解?
考点:一元一次方程的解
专题:
分析:(1)将b=1代入上式,化简即可求得方程的解;
(2)化简原式,根据0•x=0,x有无数个解即可求得a、b的值.
(2)化简原式,根据0•x=0,x有无数个解即可求得a、b的值.
解答:解:(1)b=1,代入原式得:
a(3x-2)+2x-3=8x-7,
去括号得:3ax-2a+2x-3=8x-7,
移项合并同类项得:(3a-6)x=2a-4,(a≠2)
化系数为1得:x=
.
(2)a(3x-2)+b(2x-3)=8x-7,
去括号得:3ax-2a+2bx-3b=8x-7,
移项合并同类项得:(3a+2b-8)x=2a+3b-7,
∴当3a+2b-8=0,2a+3b-7=0时,x有无数个解,
解得:b=1,a=2.
故a=2,b=1时,方程有无数个解.
a(3x-2)+2x-3=8x-7,
去括号得:3ax-2a+2x-3=8x-7,
移项合并同类项得:(3a-6)x=2a-4,(a≠2)
化系数为1得:x=
| 2 |
| 3 |
(2)a(3x-2)+b(2x-3)=8x-7,
去括号得:3ax-2a+2bx-3b=8x-7,
移项合并同类项得:(3a+2b-8)x=2a+3b-7,
∴当3a+2b-8=0,2a+3b-7=0时,x有无数个解,
解得:b=1,a=2.
故a=2,b=1时,方程有无数个解.
点评:本题考查了一元一次方程的解,根据0•x=0中x有无数个解即可求得a、b的值.

练习册系列答案
相关题目
一元一次方程
+
+
+…+
=1025的解是( )
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 3×4 |
| x |
| 1025×1026 |
| A、1024 | B、1025 |
| C、1026 | D、1027 |
 如图,AB是⊙O的直径,半径OC⊥AB,点D、E分别在OA、OC上,且OD=OE,直线BE交⊙O于点F,判断直线AF、DC的位置关系,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,点D、E分别在OA、OC上,且OD=OE,直线BE交⊙O于点F,判断直线AF、DC的位置关系,并说明理由. 如图,求∠1+∠2的值.
如图,求∠1+∠2的值.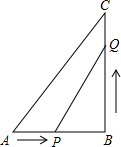 如图,△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
如图,△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.