题目内容

4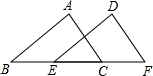．如图，在三角形ABC中，BC=8，将三角形ABC以每秒2cm的速度沿BC所在直线向右平移，所得的图形对应为三角形DEF，设平移的时间为t秒，当t=（　　）时，AD=CE．
A．1B．2C．3D．4

分析 连接AD，由平移的性质可知：AD=BE，若AD=CE，可得BE=CE，即E为BC中点时成立，进而可求出运动的时间t．

解答 解：
∵三角形DEF是由三角形ABC平移而得，
∴AD=BE，
∵AD=CE，
∴BE=CE，
∵BC=8，
∴BE=CE=4，
∵三角形ABC以每秒2cm的速度沿BC所在直线向右平移，
∴2t=4，
解得t=2，
故选B．

点评 本题考查了平移的性质，是基础题，熟记平移的性质是解题的关键．

练习册系列答案
相关题目
14．在平面直角坐标系中，O是坐标原点，点A的坐标是（-4，0），点B的坐标是（0，b）（b＞0），点P是直线AB上的一个动点，记点P关于y轴对称的点为P′．
（1）当b=3时（如图1），
①求直线AB的函数表达式．
②在x轴上找一点Q（点O除外），使△APQ与△AOB全等，直接写出点Q的所有坐标（-9，0）、（-8，0）或（1，0）
（2）若点P在第一象限（如图2），设点P的横坐标为a，作PC⊥x轴于点C，连结AP′，CP′．当△ACP′是以点P′为直角顶点的等腰直角三角形时，求出a，b的值．
（3）当线段OP′恰好被直线AB垂直平分时（如图3），直接写出b=$\frac{4\sqrt{3}}{3}$．
15．如果关于x的不等式组$\left\{\begin{array}{l}{3x-2a＞0}\\{4x-3b≤0}\end{array}\right.$的整数解仅有3，4，5，那么适合这个不等式组的整数a，b的有序数对（a，b）共有（　　）
A．2对B．4对C．6对D．8对
12．下列说法正确的是（　　）
A．四边相等的四边形是正方形
B．四角相等的四边形是正方形
C．对角线互相垂直的平行四边形是正方形
D．有一个角是直角的菱形是正方形
19．在平面直角坐标系xOy中，过点（0，2）且平行于x轴的直线，与直线y=x-1交于点A．点A关于直线x=1的对称点为B，抛物线C1：y=x2+bx+c经过点A，B．
（1）求点A，B的坐标；
（2）求抛物线C1的表达式及顶点坐标；
（3）若抛物线C2：y=ax2+1（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围．
9．若a+b=-$\frac{1}{5}$，a+3b=1，则3a2+12ab+9b2+$\frac{3}{5}$的值．
16．如图，已知射线AB与直线CD交于点O，OF平分∠BOC，OG⊥OF于O，AE∥OF．
（1）若∠A=20°，求∠DOF的度数；
（2）试说明OG平分∠BOD．
16．①设a＞b＞0，a2+b2-6ab=0，则$\frac{a+b}{a-b}$的值为$\sqrt{2}$；
②若$\frac{1}{a}-\frac{1}{b}=2$，则$\frac{2a-13ab-2b}{a-2ab-b}$=$\frac{17}{4}$．
17．将$\frac{a^2+5ab}{3a-2b}$中的a、b都扩大为原来的4倍，则分式的值（　　）
A．不变B．扩大原来的4倍C．扩大原来的8倍D．扩大原来的16倍

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网