题目内容
9.如图,正方形ABCD和正方形GCEF底边对齐,两个正方形边长分别为a和b (a>b).设S△AGE=S1,S△BDF=S2.
(1)用含a、b的代数式表示DG的长度;
(2)若DG=1,S2-S1=$\frac{7}{2}$,求BE的长度.
分析 (1)根据图形即可得到用含a、b的代数式表示DG的长度;
(2)根据题意和图形可以用含a、b的代数式表示BE的长度.
解答 解:(1)由图可得,
DG=DC-GC,
∵DC=a,GC=b,
∴DG=a-b;
(2)由题意可得,
S1=${a}^{2}+{b}^{2}-\frac{(a+b)a}{2}-\frac{{b}^{2}}{2}-\frac{a(a-b)}{2}$=$\frac{{b}^{2}}{2}$,
S2=$(a+b)a-\frac{(a+b)b}{2}-\frac{{a}^{2}}{2}-\frac{(a-b)b}{2}$=$\frac{{a}^{2}}{2}$,
∵DG=1,S2-S1=$\frac{7}{2}$,
∴$\left\{\begin{array}{l}{a-b=1}\\{\frac{{a}^{2}}{2}-\frac{{b}^{2}}{2}=\frac{7}{2}}\end{array}\right.$,
解得,a+b=7,
∴BE=a+b=7,
即BE的长度为7.
点评 本题考查整式的混合运算,解答本题的关键是明确整式的混合运算的计算方法.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
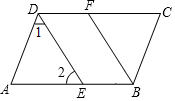 如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.
如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.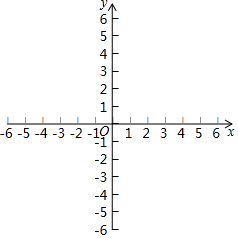 观察:点…A(-5,-2)、B(-4,-1),C(1,4)、D(2,5)、E(x,y)…;
观察:点…A(-5,-2)、B(-4,-1),C(1,4)、D(2,5)、E(x,y)…;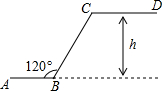 如图是某商场一楼与二楼之间手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=120°,BC的长是8m,则乘电梯从点B到点C上升的高度h是4$\sqrt{3}$m.
如图是某商场一楼与二楼之间手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=120°,BC的长是8m,则乘电梯从点B到点C上升的高度h是4$\sqrt{3}$m.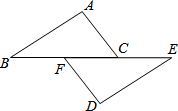 已知:点B、F、C、E在同一条直线上,FB=CE,AC=DF,现给出下列条件:①AB=ED;②∠A=∠D=90°;③∠ACB=∠DFE.请你从上面三个条件中选择一个合适的条件,添加到已知条件中,使得AB∥ED成立,并给出证明.
已知:点B、F、C、E在同一条直线上,FB=CE,AC=DF,现给出下列条件:①AB=ED;②∠A=∠D=90°;③∠ACB=∠DFE.请你从上面三个条件中选择一个合适的条件,添加到已知条件中,使得AB∥ED成立,并给出证明.