题目内容
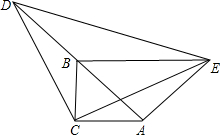 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.(1)求证:△ACE≌△BCD;
(2)若AC=3,求BE的长.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)首先证明∠DCB=∠ECA,然后利用SAS即可证明两个三角形全等;
(2)首先证明∠BAE=90°,则△ABE是等腰直角三角形,则利用勾股定理即可求解.
(2)首先证明∠BAE=90°,则△ABE是等腰直角三角形,则利用勾股定理即可求解.
解答:(1)证明:∵∠DCE=∠BCA=90°,
∴∠DCB=∠ECA,
则在△ACE和△BCD中,
,
∴△ACE≌△BCD;
(2)解:∵△ABC是等腰直角三角形,
∴AB=
AB=3
,∠ABC=∠BAC=45°,
∴∠CBD=135°,
∵△ACE≌△BCD,
∴BD=AE=AB=3
,∠CAE=∠CBD=135°,
∴∠BAE=135°-45°=90°.
∴△ABE是等腰直角三角形.
∴BE=
AB=
×3
=6.
∴∠DCB=∠ECA,
则在△ACE和△BCD中,
|
∴△ACE≌△BCD;
(2)解:∵△ABC是等腰直角三角形,
∴AB=
| 2 |
| 2 |
∴∠CBD=135°,
∵△ACE≌△BCD,
∴BD=AE=AB=3
| 2 |
∴∠BAE=135°-45°=90°.
∴△ABE是等腰直角三角形.
∴BE=
| 2 |
| 2 |
| 2 |
点评:本题考查了全等三角形的判定与性质以及勾股定理的应用,正确证明△ABE是等腰直角三角形是关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=10,BC=30,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=10,BC=30,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0). 已知:△ABC中,∠ABC=2∠ACB,∠ABC的平分线BD与∠ACB的平分线CD相交于点D,且CD=AB,求证:∠A=60°.
已知:△ABC中,∠ABC=2∠ACB,∠ABC的平分线BD与∠ACB的平分线CD相交于点D,且CD=AB,求证:∠A=60°. 在活动课上,小明和小红合作用一副三角板来测量学校旗杆MN的高度,在旗杆一侧的地面上,小明按如图所示的方式放置含45°的三角板,并调整其位置,使斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°,在旗杆另一侧的地面上,小红用同样的方法测得旗杆顶端M的仰角为30°,此时,两人相距28m,且点A,N,B在同一条直线上,请你求出旗杆MN的高度(参考数据:
在活动课上,小明和小红合作用一副三角板来测量学校旗杆MN的高度,在旗杆一侧的地面上,小明按如图所示的方式放置含45°的三角板,并调整其位置,使斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°,在旗杆另一侧的地面上,小红用同样的方法测得旗杆顶端M的仰角为30°,此时,两人相距28m,且点A,N,B在同一条直线上,请你求出旗杆MN的高度(参考数据: 如图,在⊙O中,AD、BC相交于点E,AD=CB.求证:
如图,在⊙O中,AD、BC相交于点E,AD=CB.求证: 如图,AC是⊙O的直径,AB、CD是⊙O的两条弦,且
如图,AC是⊙O的直径,AB、CD是⊙O的两条弦,且
 如图,在△ABC中,∠B=2∠C,AB=5,AC=9,求BC的长.
如图,在△ABC中,∠B=2∠C,AB=5,AC=9,求BC的长.