题目内容
在活动课上，小明和小红合作用一副三角板来测量学校旗杆MN的高度，在旗杆一侧的地面上，小明按如图所示的方式放置含45°的三角板，并调整其位置，使斜边与旗杆顶端M在同一条直线上，测得旗杆顶端M的仰角为45°，在旗杆另一侧的地面上，小红用同样的方法测得旗杆顶端M的仰角为30°，此时，两人相距28m，且点A，N，B在同一条直线上，请你求出旗杆MN的高度（参考数据：| 2 |
| 3 |
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：根据题意可知MN⊥AB，设MN=xm，分别在△AMN和△BMN中表示出AN、BN，然后根据两人相距AB=28m，列方程求解．
解答：解：由题意得，MN⊥AB于点N，设MN=xm．
在Rt△AMN中，
∵∠ANM=90°，∠MAN=45°，
∴∠AMN=∠MAN=45°．
∴AN=MN=xm，
在Rt△BMN中，
∵∠BNM=90°，∠MBN=30°，
∴tan∠MBN=
，
即tan30°=
，
∴BN=
x，
∵AB=28m，
∴AN+BN=28m，
∴x+
x=28，
解得：x=14（
-1）≈10．
答：旗杆MN的高度约为10m．
在Rt△AMN中，
∵∠ANM=90°，∠MAN=45°，
∴∠AMN=∠MAN=45°．
∴AN=MN=xm，
在Rt△BMN中，
∵∠BNM=90°，∠MBN=30°，
∴tan∠MBN=
| MN |
| BN |
即tan30°=
| x |
| BN |
∴BN=
| 3 |
∵AB=28m，
∴AN+BN=28m，
∴x+
| 3 |
解得：x=14（
| 3 |
答：旗杆MN的高度约为10m．
点评：本题考查了解直角三角形的应用，解答本题的关键是根据所给的仰角构造直角三角形，利用三角函数的知识求解直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB，AO为邻边作?AOC1B，对角线交于点O1；以AB，AO1为邻边作?AO1C2B；…；以此类推，则?AOn-1CnB的面积为
如图，在矩形ABCD中，AB=6，BC=8，沿直线MN对折，使A、C重合，直线MN交AC于O．
如图，AB=AC，AD=AE，∠ADE=∠B．求证：BD=CE．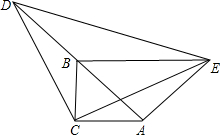
如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰直角三角形CDE，其中∠DCE=90°，连接BE．
定滑轮的起重装置如图所示，滑轮半径为12cm，当重物上升4πcm时，滑轮的半径OA按逆时针方向旋转的度数是（假设绳索与滑轮之间没有滑动）
二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2，下列结论：①abc＞0；②9a+c＞3b；③4a+b=0；④当x＞-1时，y的值随x值的增大而增大．其中正确的结论有（ ）
如图1，Rt△ABC≌Rt△ADC，∠B=∠D=90°．