题目内容
 如图,在⊙O中,AD、BC相交于点E,AD=CB.求证:
如图,在⊙O中,AD、BC相交于点E,AD=CB.求证:(1)OE平分∠AEC;
(2)BE=DE.
考点:圆心角、弧、弦的关系
专题:证明题
分析:(1)连接AB、DC、EO、AO、CO、AC,根据AD=CB可得∠BAC=∠DCA,然后证明△BAC≌△DCA可得AB=CD,再证明△BAE≌△DCE可得AE=CE,最后再证明△AEO≌△CEO可得∠AEO=∠CEO,进而可得OE平分∠AEC;
(2)根据AD=CB,AE=CE,利用等式的性质可得BE=DE.
(2)根据AD=CB,AE=CE,利用等式的性质可得BE=DE.
解答: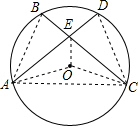 证明:(1)连接AB、DC、EO、AO、CO、AC,
证明:(1)连接AB、DC、EO、AO、CO、AC,
∵AD=CB,
∴∠BAC=∠DCA,
在△ABC和△DCA中,
,
∴△BAC≌△DCA(AAS),
∴AB=CD,
在△BAE和△DCE中,
,
∴△BAE≌△DCE(AAS),
∴AE=CE,
在△AEO和△CEO中,
,
∴△AEO≌△CEO(SSS),
∴∠AEO=∠CEO,
∴OE平分∠AEC;
(2)∵AD=CB,AE=CE,
∴AD-AE=CB-CE,
∴BE=DE.
 证明:(1)连接AB、DC、EO、AO、CO、AC,
证明:(1)连接AB、DC、EO、AO、CO、AC,∵AD=CB,
∴∠BAC=∠DCA,
在△ABC和△DCA中,
|
∴△BAC≌△DCA(AAS),
∴AB=CD,
在△BAE和△DCE中,
|
∴△BAE≌△DCE(AAS),
∴AE=CE,
在△AEO和△CEO中,
|
∴△AEO≌△CEO(SSS),
∴∠AEO=∠CEO,
∴OE平分∠AEC;
(2)∵AD=CB,AE=CE,
∴AD-AE=CB-CE,
∴BE=DE.
点评:此题主要考查了全等三角形的判定与性质,以及圆心角、弧、弦的关系,关键是掌握全等三角形的判定与性质.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
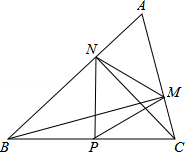 如图,在△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②
如图,在△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②| AM |
| AB |
| AN |
| AC |
| A、①②③ | B、①③④ |
| C、①②④ | D、②③④ |
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①abc>0;②9a+c>3b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①abc>0;②9a+c>3b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |




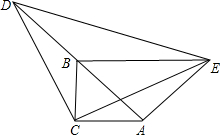 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE. 如图,长春市某中学学生小刚在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得窗户A处到底面的距离AB为20米,树顶C处的俯角为44°,楼底到大树的距离BD为12米,求树CD的高度.(保留小数点后一位,参考数据:sin44°≈0.69,cos44°≈0.72,tan44°≈0.97)
如图,长春市某中学学生小刚在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得窗户A处到底面的距离AB为20米,树顶C处的俯角为44°,楼底到大树的距离BD为12米,求树CD的高度.(保留小数点后一位,参考数据:sin44°≈0.69,cos44°≈0.72,tan44°≈0.97) 如图,在梯形ABCD中,∠ABC=90°,AE∥CD交BC于E,O是AC的中点,AB=
如图,在梯形ABCD中,∠ABC=90°,AE∥CD交BC于E,O是AC的中点,AB= 如图,直线AB,CD相交于点O,EO⊥CD于O,OE平分∠BOF,∠1=65°,求∠BOF的度数.
如图,直线AB,CD相交于点O,EO⊥CD于O,OE平分∠BOF,∠1=65°,求∠BOF的度数.