题目内容
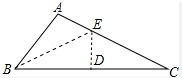
 如图,在△ABC中,∠B=2∠C,AB=5,AC=9,求BC的长.
如图,在△ABC中,∠B=2∠C,AB=5,AC=9,求BC的长.考点:相似三角形的判定与性质,角平分线的性质
专题:
分析:由线段的垂直平分线性质得出BE=CE,得出∠EBD=∠C,证出∠ABE=∠C,因此△ABE∽△ACB,得比例式
=
=
,先求出AE,再求出CE=BE=
,即可求出BC的长.
| AB |
| AC |
| AE |
| AB |
| BE |
| BC |
| 56 |
| 9 |
解答:解:过BC的中点D作DE⊥BC交AC于E,连接BE;如图所示:
 则BE=CE,
则BE=CE,
∴∠EBD=∠C,
∵∠ABC=2∠C,
∴∠ABE=∠C,
又∵∠A=∠A,
∴△ABE∽△ACB,
∴
=
=
,
∴AB2=AE•AC,
∴AE=
=
=
,
∴CE=9-
=
,
∴BE=
,
∴
=
,
∴BC=
.
 则BE=CE,
则BE=CE,∴∠EBD=∠C,
∵∠ABC=2∠C,
∴∠ABE=∠C,
又∵∠A=∠A,
∴△ABE∽△ACB,
∴
| AB |
| AC |
| AE |
| AB |
| BE |
| BC |
∴AB2=AE•AC,
∴AE=
| AB2 |
| AC |
| 52 |
| 9 |
| 25 |
| 9 |
∴CE=9-
| 25 |
| 9 |
| 56 |
| 9 |
∴BE=
| 56 |
| 9 |
∴
| 5 |
| 9 |
| ||
| BC |
∴BC=
| 56 |
| 5 |
点评:本题考查了线段垂直平分线的性质和相似三角形的判定与性质;证明三角形相似得出比例式分别求出相关线段的长是解题关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下列计算正确的是( )
| A、a2=-a2 | ||||||
| B、(x+1)2=x2+1 | ||||||
C、3
| ||||||
| D、(3a3)2=6a6 |
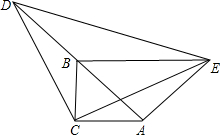 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE. 如图,直线AB,CD相交于点O,EO⊥CD于O,OE平分∠BOF,∠1=65°,求∠BOF的度数.
如图,直线AB,CD相交于点O,EO⊥CD于O,OE平分∠BOF,∠1=65°,求∠BOF的度数. 如图所示,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.
如图所示,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE. 如图1,Rt△ABC≌Rt△ADC,∠B=∠D=90°.
如图1,Rt△ABC≌Rt△ADC,∠B=∠D=90°. 如图,E是正方形ABCD中AB边的中点,F是边AD的四等分点.画出△AEF关于正方形ABCD的中心对称的三角形.
如图,E是正方形ABCD中AB边的中点,F是边AD的四等分点.画出△AEF关于正方形ABCD的中心对称的三角形.