题目内容
已知一元二次方程y2-3y+1=0的两个实数根分别为y1,y2,则(y1-1)(y2-2)的值为 .
考点:根与系数的关系
专题:计算题
分析:根据根与系数的关系得到y1+y2=3,y1•y2=1,再把(y1-1)(y2-2)展开整理得到y1•y2-3(y1+y2)+2,然后利用整体代入的方法进行计算.
解答:解:根据题意得y1+y2=3,y1•y2=1,
所以(y1-1)(y2-2)=y1•y2-3(y1+y2)+2=1-3×3+2=-6.
故答案为-6.
所以(y1-1)(y2-2)=y1•y2-3(y1+y2)+2=1-3×3+2=-6.
故答案为-6.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
同一坐标系中,抛物线y=(x-a)2与直线y=a+ax的图象可能是( )
A、 |
B、 |
C、 |
D、 |
若y=(m2+3m+2)xm2+m为二次函数,则m的值为( )
| A、-2 或1 | B、-2 |
| C、-1 | D、1 |
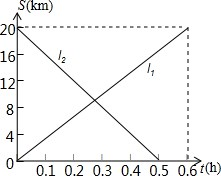 甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表 示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表 示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.  如图,根据∠1=∠2,小刚得出了下列结论:
如图,根据∠1=∠2,小刚得出了下列结论: