题目内容
阅读下列因式分解的过程,再回答所提出的问题:
(1)上述因式分解的方法是 ,共应用了 次.
(2)将下列多项式因式分解:1+x+x(x+1)+x(x+1)2+x(x+1)3.
(3)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2013,则需应用上述方法 次,结果是 .
|
(1)上述因式分解的方法是
(2)将下列多项式因式分解:1+x+x(x+1)+x(x+1)2+x(x+1)3.
(3)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2013,则需应用上述方法
考点:因式分解-提公因式法
专题:阅读型,规律型
分析:(1)观察因式分解过程得到所用的方法为提取公因式法,共提取了2次;
(2)原式提取公因式即可得到结果;
(3)归纳总结得到一般性规律,即可得到结果.
(2)原式提取公因式即可得到结果;
(3)归纳总结得到一般性规律,即可得到结果.
解答:解:(1)上述因式分解的方法是提取公因式法,共应用了2次;
(2)原式=(1+x)[1+x+x(x+1)+x(x+1)2]
=(1+x)2[1+x+x(1+x)]
=(1+x)3(1+x)
=(x+1)4;
(3)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2013,
则需应用上述方法2013次,结果是(x+1)2014.
故答案为:(1)提取公因式法;2;(3)2013;(x+1)2014
(2)原式=(1+x)[1+x+x(x+1)+x(x+1)2]
=(1+x)2[1+x+x(1+x)]
=(1+x)3(1+x)
=(x+1)4;
(3)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2013,
则需应用上述方法2013次,结果是(x+1)2014.
故答案为:(1)提取公因式法;2;(3)2013;(x+1)2014
点评:此题考查了因式分解-提取公因式法,弄清题中的规律是解本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 找出图中的轴对称图形,并找出两对对应点、两对对应线段、两对对应角.
找出图中的轴对称图形,并找出两对对应点、两对对应线段、两对对应角. 如图是一块破碎的圆形木盖,试确定它的圆心.
如图是一块破碎的圆形木盖,试确定它的圆心.
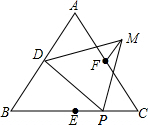 如图,D,E,F分别是正三角形ABC的边AB,BC,AC的中点,P为BC上任意一点,△DPM为正三角形.求证:PE=FM.
如图,D,E,F分别是正三角形ABC的边AB,BC,AC的中点,P为BC上任意一点,△DPM为正三角形.求证:PE=FM. 如图,PA=PB,PC是△PAB的中线,∠A=55°.求∠B的度数.
如图,PA=PB,PC是△PAB的中线,∠A=55°.求∠B的度数.