题目内容
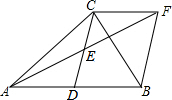 如图,在△ABC中,D是AB的中点,E是CD的中点,延长AE到F点,使得E是AF的中点,连接BF,CF.求证:DC=BF.
如图,在△ABC中,D是AB的中点,E是CD的中点,延长AE到F点,使得E是AF的中点,连接BF,CF.求证:DC=BF.考点:平行四边形的判定与性质
专题:证明题
分析:通过证△CEF≌△DEA得到:∠1=∠2,CF=DA;则易证四边形CDBF为平行四边形,然后根据“平行四边形的对边相等”的性质证得结论.
解答: 证明:如图,∵E是CD的中点,E是AF的中点,
证明:如图,∵E是CD的中点,E是AF的中点,
∴CE=DE,AE=FE,
在△CEF与△DEA中,
,
∴△CEF≌△DEA(SAS),
∴∠1=∠2,CF=DA,
∴CF∥AB,则CF∥DB
又∵E是CD的中点,
∴DA=DB,
∴CF=DB,
∴四边形CDBF是平行四边形,
∴DC=BF.
 证明:如图,∵E是CD的中点,E是AF的中点,
证明:如图,∵E是CD的中点,E是AF的中点,∴CE=DE,AE=FE,
在△CEF与△DEA中,
|
∴△CEF≌△DEA(SAS),
∴∠1=∠2,CF=DA,
∴CF∥AB,则CF∥DB
又∵E是CD的中点,
∴DA=DB,
∴CF=DB,
∴四边形CDBF是平行四边形,
∴DC=BF.
点评:本题考查了平行线的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
若x1,x2是一元二次方程2x2+4x-5=0的两个实数根,则x1+x2的值为( )
| A、2 | B、-2 | C、4 | D、-4 |
 已知△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=40,求DB的长.
已知△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=40,求DB的长.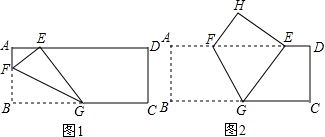
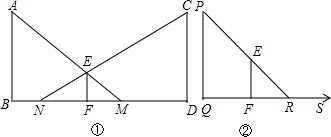
 找出图中的轴对称图形,并找出两对对应点、两对对应线段、两对对应角.
找出图中的轴对称图形,并找出两对对应点、两对对应线段、两对对应角.