题目内容
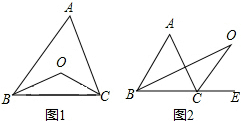
15. 如图,在Rt△ABC中,∠C=90°,AC=6,∠A的平分线交BC于点D,DE⊥AB于点E,且BE=4,求DE的长.
如图,在Rt△ABC中,∠C=90°,AC=6,∠A的平分线交BC于点D,DE⊥AB于点E,且BE=4,求DE的长.
分析 直接利用角平分线的性质结合全等三角形的判定与性质得出AC=AE,进而利用勾股定理得出DE的长.
解答  解:∵∠C=90°,∠A的平分线交BC于点D,DE⊥AB于点E,
解:∵∠C=90°,∠A的平分线交BC于点D,DE⊥AB于点E,
∴DC=DE,
在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{AD=AD}\\{DC=DE}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE=6,
∵BE=4,
∴AB=10,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=8,
设DC=DE=x,则BD=8-x,
故在Rt△BDE中,
BD2=DE2+BE2,
则(8-x)2=x2+42,
解得:x=3,
即DE=3.
点评 此题主要考查了勾股定理以及全等三角形的判定与性质,正确得出BC的长是解题关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
7.下列等式不正确的是( )
| A. | 由x=y,得到x+2=y+2 | B. | 由2a=b,得到a=b-a | ||
| C. | 由m=n,得到2m=2n | D. | 由am=an,得到m=n |
4.某地今年10月份某一周的日最高气温(单位:℃)分别为22,21,18,20,19,18,15,则这周的日最高气温的平均值为( )
| A. | 18℃ | B. | 19℃ | C. | 20℃ | D. | 21℃ |
5.下列说法错误的是( )
| A. | 4的算术平方根是2 | B. | 16的平方根是±4 | ||
| C. | 5是25的平方根 | D. | (-6)2的平方根是-6 |
 如图,数轴上的点A所表示的分数是1$\frac{2}{5}$.
如图,数轴上的点A所表示的分数是1$\frac{2}{5}$.