题目内容
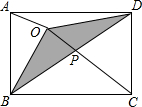 如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.
如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.考点:矩形的性质
专题:
分析:过O作MN⊥AD,交BC于N,交AD于M,EF⊥AB交AB于E,交CD于F,根据矩形的性质求出MN=AB=CD,EF=AD=BC,求出△AOD的面积+△BOC的面积=△AOB的面积+△DOC的面积,设△AOD的面积是xcm2,求出△ABD的面积,即可求出答案.
解答: 解:过O作MN⊥AD,交BC于N,交AD于M,EF⊥AB交AB于E,交CD于F,
解:过O作MN⊥AD,交BC于N,交AD于M,EF⊥AB交AB于E,交CD于F,
∵四边形ABCD是矩形,
∴AD=BC,AB=CD,AD∥BC,AB∥CD,
∴EF⊥CD,MN⊥BC,
则∠DAB=∠ABC=∠BNM=90°,
∴四边形ABNM是矩形,
∴MN=AB=CD,
同理EF=AD=BC,
∵S△AOD+S△BOC=
AD×OM+
BC×ON=
AD×AB=
S矩形ABCD,
同理S△AOB+S△DOC=
S矩形ABCD,
∴S△AOD+S△BOC=S△AOB+S△DOC=
S矩形ABCD,
设△AOD的面积是xcm2,
∵△OBC的面积是5cm2,△OAB的面积是2cm2,
∴△ODC的面积=(5+x)-2=(3+x)(cm2),
∴S矩形ABCD=5+2+3+x+x=(10+2x)(cm2),
∴S△ABD=S△CBD=
S矩形ABCD=(5+x)cm2,
∴S△BOD=S△ABD-S△AOD-S△AOB=5+x-x-2=3(cm2),
即△OBD的面积是3cm2.
 解:过O作MN⊥AD,交BC于N,交AD于M,EF⊥AB交AB于E,交CD于F,
解:过O作MN⊥AD,交BC于N,交AD于M,EF⊥AB交AB于E,交CD于F,∵四边形ABCD是矩形,
∴AD=BC,AB=CD,AD∥BC,AB∥CD,
∴EF⊥CD,MN⊥BC,
则∠DAB=∠ABC=∠BNM=90°,
∴四边形ABNM是矩形,
∴MN=AB=CD,
同理EF=AD=BC,
∵S△AOD+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同理S△AOB+S△DOC=
| 1 |
| 2 |
∴S△AOD+S△BOC=S△AOB+S△DOC=
| 1 |
| 2 |
设△AOD的面积是xcm2,
∵△OBC的面积是5cm2,△OAB的面积是2cm2,
∴△ODC的面积=(5+x)-2=(3+x)(cm2),
∴S矩形ABCD=5+2+3+x+x=(10+2x)(cm2),
∴S△ABD=S△CBD=
| 1 |
| 2 |
∴S△BOD=S△ABD-S△AOD-S△AOB=5+x-x-2=3(cm2),
即△OBD的面积是3cm2.
点评:本题考查了矩形的性质和判定的应用,解此题的关键是求出S△AOD+S△BOC=S△AOB+S△DOC=
S矩形ABCD,题目比较好,有一定的难度.
| 1 |
| 2 |

练习册系列答案
相关题目
下列方程中是一元一次方程的是( )
| A、-5x+4=3y2 | ||||
| B、5(m2-1)=1-5m2 | ||||
C、2-
| ||||
| D、2(3p-2)=2p2 |
 如图,△ABC中,∠C=90°,∠CBA=30°,BC=20
如图,△ABC中,∠C=90°,∠CBA=30°,BC=20 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,则△BCD与△ABC的周长之比为
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,则△BCD与△ABC的周长之比为 如图,由单位正方形拼成的“工“字形中,顶点为小正方形顶点的等腰直角三角形有
如图,由单位正方形拼成的“工“字形中,顶点为小正方形顶点的等腰直角三角形有