题目内容
己知⊙O的弦AB=2cm,圆心到AB的距离为n cm,则⊙O的半径R= ,⊙O的周长为 ,⊙O的面积为 .
考点:垂径定理,勾股定理
专题:计算题
分析:作OC⊥AB于C,连结OA,如图,则OC=ncm,根据垂径定理得AC=
AB=1,在Rt△AOC中,利用勾股定理得到OA=
,即⊙O的半径R为
cm,然后根据圆的周长公式和面积公式求解.
| 1 |
| 2 |
| n2+1 |
| n2+1 |
解答:解:作OC⊥AB于C,连结OA,如图,则OC=n,
∵OC⊥AB,
∴AC=BC=
AB=
•2=1,
在Rt△AOC中,OA=
=
,
即⊙O的半径R为
cm,
∴,⊙O的周长为2π
cm,
⊙O的面积为πR2=(πn2+π)cm2.
故答案为
cm,2π
cm,(πn2+π)cm2.

∵OC⊥AB,
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOC中,OA=
| OC2+AC2 |
| n2+1 |
即⊙O的半径R为
| n2+1 |
∴,⊙O的周长为2π
| n2+1 |
⊙O的面积为πR2=(πn2+π)cm2.
故答案为
| n2+1 |
| n2+1 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 墨墨在如图所示的△ABC的基础上作图,步骤如下:①分别以点A和点B为圆心,以a(a>
墨墨在如图所示的△ABC的基础上作图,步骤如下:①分别以点A和点B为圆心,以a(a>| 1 |
| 2 |
| 1 |
| 2 |
| A、AO=BO=CO |
| B、点O是△ABC的重心 |
| C、∠AOB=∠BOC |
| D、CO平分∠ACB |
向上发射一枚炮弹,经x秒后的高度为y,且时间与高度的关系式为y=ax2+bx,若此时炮弹在第7秒与第13秒时的高度相等,则在下列哪一个时间的高度是最高的( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
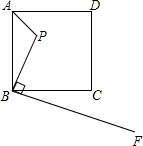 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.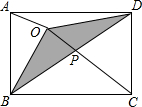 如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.
如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.