题目内容
 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,则△BCD与△ABC的周长之比为
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,则△BCD与△ABC的周长之比为考点:相似三角形的判定与性质
专题:
分析:根据已知条件先证出△BCD∽△BAC,根据∠B=60°,得出∠BCD=∠A=30°,求出BC=2BD,即可得出△BCD与△ABC的相似比为1:2,再根据相似三角形的周长比等于相似比,从而得出答案.
解答:解:∵CD⊥AB,
∴∠BDC=90°,
∵∠B=∠B,∠BDC=∠BCA=90°,
∴△BCD∽△BAC,
∵∠B=60°,
∴∠BCD=∠A=30°,
在Rt△BCD中,∠BCD=30°,则BC=2BD,
∴C△BCD:C△ABC=BD:BC=1:2;
故答案为:1:2.
∴∠BDC=90°,
∵∠B=∠B,∠BDC=∠BCA=90°,
∴△BCD∽△BAC,
∵∠B=60°,
∴∠BCD=∠A=30°,
在Rt△BCD中,∠BCD=30°,则BC=2BD,
∴C△BCD:C△ABC=BD:BC=1:2;
故答案为:1:2.
点评:此题考查了相似三角形的判定与性质,用到的知识点是相似三角形的判定与性质,相似三角形的周长比等于相似比,面积比等于相似比的平方,关键是求出BC=2BD.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
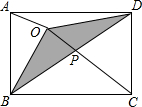 如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.
如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积. “十一”黄金周期间,某游乐园在7天假期中每天游园的人数变化如下表:
“十一”黄金周期间,某游乐园在7天假期中每天游园的人数变化如下表: