题目内容
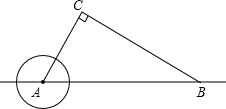 如图,△ABC中,∠C=90°,∠CBA=30°,BC=20
如图,△ABC中,∠C=90°,∠CBA=30°,BC=20| 3 |
(1)求AB的长.
(2)一个圆心在A点,半径为6的圆以2个单位长度每秒的速度向右运动,在运动过程中,圆心始终都在直线AB上,问运动多少秒时,圆与△ABC的一边所在的直线相切?
考点:切线的性质
专题:分类讨论
分析:(1)根据含30度的直角三角形三边的关系易求得AB=40;
(2)如图,当圆心运动点D时与直线AC相切于点P,圆心运动点E时与直线BC相切于点M,圆心运动点F时与直线BC相切于点N,连结DP,EM,FN,根据切线的性质得DP⊥AC,EM⊥BC,FN⊥BC,DP=EM=FN=6,在Rt△ADP中根据含30度的直角三角形三边的关系可求出PA=
PD=2
,则AD=2PA=4
,然后计算圆运动的时间;在Rt△EBM中易得EB=2EM=12,则AE=AB-EB=28,于是可计算圆运动的时间;在Rt△EBM中,由于∠FBN=∠ABC=30°,则易得BF=2FN=12,所以AF=AB+FB=52,然后计算圆运动的时间.
(2)如图,当圆心运动点D时与直线AC相切于点P,圆心运动点E时与直线BC相切于点M,圆心运动点F时与直线BC相切于点N,连结DP,EM,FN,根据切线的性质得DP⊥AC,EM⊥BC,FN⊥BC,DP=EM=FN=6,在Rt△ADP中根据含30度的直角三角形三边的关系可求出PA=
| ||
| 3 |
| 3 |
| 3 |
解答:解:(1)∵∠C=90°,∠CBA=30°,
∴AC=
BC=20,
∴AB=2BC=40;
(2) 如图,当圆心运动点D时与直线AC相切于点P,圆心运动点E时与直线BC相切于点M,圆心运动点F时与直线BC相切于点N,
如图,当圆心运动点D时与直线AC相切于点P,圆心运动点E时与直线BC相切于点M,圆心运动点F时与直线BC相切于点N,
连结DP,EM,FN,则DP⊥AC,EM⊥BC,FN⊥BC,DP=EM=FN=6,
在Rt△ADP中,∵∠PAD=60°,
∴∠ADP=30°,
∴PA=
PD=
•6=2
,
∴AD=2PA=4
,
∴圆运动的时间=
=2
(秒);
在Rt△EBM中,∵∠EBM=30°,
∴EB=2EM=12,
∴AE=AB-EB=28,
∴圆运动的时间=
=14(秒);
在Rt△EBM中,∵∠FBN=∠ABC=30°,
∴BF=2FN=12,
∴AF=AB+FB=52,
∴圆运动的时间=
=26(秒),
综上所述,运动2
秒或14秒或26秒时,圆与△ABC的一边所在的直线相切.
∴AC=
| ||
| 3 |
∴AB=2BC=40;
(2)
 如图,当圆心运动点D时与直线AC相切于点P,圆心运动点E时与直线BC相切于点M,圆心运动点F时与直线BC相切于点N,
如图,当圆心运动点D时与直线AC相切于点P,圆心运动点E时与直线BC相切于点M,圆心运动点F时与直线BC相切于点N,连结DP,EM,FN,则DP⊥AC,EM⊥BC,FN⊥BC,DP=EM=FN=6,
在Rt△ADP中,∵∠PAD=60°,
∴∠ADP=30°,
∴PA=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴AD=2PA=4
| 3 |
∴圆运动的时间=
4
| ||
| 2 |
| 3 |
在Rt△EBM中,∵∠EBM=30°,
∴EB=2EM=12,
∴AE=AB-EB=28,
∴圆运动的时间=
| 28 |
| 2 |
在Rt△EBM中,∵∠FBN=∠ABC=30°,
∴BF=2FN=12,
∴AF=AB+FB=52,
∴圆运动的时间=
| 52 |
| 2 |
综上所述,运动2
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 墨墨在如图所示的△ABC的基础上作图,步骤如下:①分别以点A和点B为圆心,以a(a>
墨墨在如图所示的△ABC的基础上作图,步骤如下:①分别以点A和点B为圆心,以a(a>| 1 |
| 2 |
| 1 |
| 2 |
| A、AO=BO=CO |
| B、点O是△ABC的重心 |
| C、∠AOB=∠BOC |
| D、CO平分∠ACB |
 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.(不写作法,保留作图痕迹.)
如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.(不写作法,保留作图痕迹.)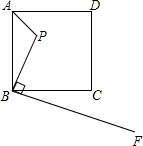 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.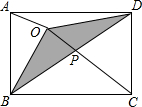 如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.
如图所示,O是长方形ABCD内一点,已知△OBC的面积是5cm2,△OAB的面积是2cm2,求△OBD的面积.