题目内容
9. 如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作FM∥AD交AC于F,求FC的长.
如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作FM∥AD交AC于F,求FC的长.
分析 过点B作BE∥AC与AD的延长线交于一点E,由AD平分∠BAC,先证出BA=BE,△BDE∽△CAD,得到$\frac{BD}{DC}=\frac{BE}{AC}=\frac{AB}{AC}=\frac{4}{7}$,再由M是BC的中点,得到$\frac{CM}{CD}=\frac{11}{14}$,然后由FM∥AD得到$\frac{CF}{AC}=\frac{CM}{CD}=\frac{11}{14}$,从而得到CF=$\frac{11}{2}$.
解答 解:如图所示,过点B作BE∥AC与AD的延长线交于一点E,
∴∠E=∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠E=∠BAD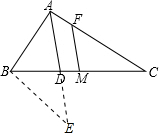 ,
,
∴AB=BE,
又∵△BDE∽△CAD,
∴$\frac{BD}{DC}=\frac{BE}{AC}=\frac{AB}{AC}=\frac{4}{7}$,
∵M是BC的中点,
∴$\frac{CM}{CD}=\frac{11}{14}$,
∵FM∥AD,
∴$\frac{CF}{AC}=\frac{CM}{CD}=\frac{11}{14}$,
∴$\frac{CF}{7}=\frac{11}{14}$,
∴CF=$\frac{11}{2}$.
点评 本题主要考查了平行线的性质、相似三角形的判定与性质的综合运用,作出辅助线构造相似三角形,转移线段比是本题的关键.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
14.使分式$\frac{x}{2x-4}$有意义的x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | x=-2 | D. | x≠-2 |
 重庆一中皇冠实验中学于4月16日顺利完成了中招体考.为了了解体考测试成绩,从初三学生中随机调查了若干名学生,调查结果分以下四种:“50”、“48-49”、“46-47”、“45及以下”,分别记为“A”、“B”、“C”、“D”.其中得分为“B”的有5人,得分为“C”的有1人,根据调查结果绘制了如下不完整的扇形统计图,请你根据统计图提供的信息解答以下问题:
重庆一中皇冠实验中学于4月16日顺利完成了中招体考.为了了解体考测试成绩,从初三学生中随机调查了若干名学生,调查结果分以下四种:“50”、“48-49”、“46-47”、“45及以下”,分别记为“A”、“B”、“C”、“D”.其中得分为“B”的有5人,得分为“C”的有1人,根据调查结果绘制了如下不完整的扇形统计图,请你根据统计图提供的信息解答以下问题: 如图,在五边形ABCDE中,点M、N分别在AB、AE的边上.∠1+∠2=100°,则∠B+∠C+∠D+∠E=460°.
如图,在五边形ABCDE中,点M、N分别在AB、AE的边上.∠1+∠2=100°,则∠B+∠C+∠D+∠E=460°. 如图,在矩形ABCD中,AB+1=BC,点E在CD,且3DE=DC,现有一动点P从点A出发,沿路径A,B,C,E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图形表示大致是( )
如图,在矩形ABCD中,AB+1=BC,点E在CD,且3DE=DC,现有一动点P从点A出发,沿路径A,B,C,E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图形表示大致是( )



 已知,如图,正方形ABCD中,E是AB的中点,∠CEF=∠ECD.F在CD的延长线上,EF交AD于点P,求证:AP=2PD.
已知,如图,正方形ABCD中,E是AB的中点,∠CEF=∠ECD.F在CD的延长线上,EF交AD于点P,求证:AP=2PD.