题目内容
13. 已知,⊙O与正六边形0ABCDE的边0A、0E分别交于点F、G,则弧FG所对的圆周角∠FPG的正弦值为$\frac{\sqrt{3}}{2}$.
已知,⊙O与正六边形0ABCDE的边0A、0E分别交于点F、G,则弧FG所对的圆周角∠FPG的正弦值为$\frac{\sqrt{3}}{2}$.
分析 先根据正六边形的性质求出∠FOG的度数,再由圆周角定理求出∠P的度数,根据特殊角的三角函数值即可得出结论.
解答 解:∵六边形0ABCDE是正六边形,
∴∠FOG=120°,
∴∠FPG=60°,
∴sin∠FPG=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{3}}}{2}$.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
3. 有理数a、b在数轴上的位置如图所示,则下列各式的符号为负的是( )
有理数a、b在数轴上的位置如图所示,则下列各式的符号为负的是( )
 有理数a、b在数轴上的位置如图所示,则下列各式的符号为负的是( )
有理数a、b在数轴上的位置如图所示,则下列各式的符号为负的是( )| A. | a-b | B. | -ab | C. | b-a | D. | a4b4 |
5.下列根式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{18}$ |
2.代数式1-$\frac{{x}^{2}}{x}$是( )
| A. | 单项式 | B. | 多项式 | C. | 分式 | D. | 整式 |
3.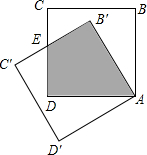 如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )
如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )
 如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )
如图,边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′,则图中阴影部分面积为( )| A. | 1-$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 1-$\frac{2\sqrt{3}}{3}$ |
 如图,一天我国一渔政船航行到A处时,发现在南偏东60°方向,相距20海里的P处有一可疑渔船,正沿西南方向向我领海区域航行,我渔政船立即沿正南方向航行拦截,2小时后,在我领海区域的B处截获可疑渔船.请求出我渔政船从A处航行到B处的航程(结果保留根号).
如图,一天我国一渔政船航行到A处时,发现在南偏东60°方向,相距20海里的P处有一可疑渔船,正沿西南方向向我领海区域航行,我渔政船立即沿正南方向航行拦截,2小时后,在我领海区域的B处截获可疑渔船.请求出我渔政船从A处航行到B处的航程(结果保留根号).