题目内容
14．绝对值小于$\sqrt{6}$的整数有5个．分析 首先得出2＜$\sqrt{6}$＜3，进而利用绝对值得出符合题意的答案．
解答 解：∵2＜$\sqrt{6}$＜3，
∴绝对值小于$\sqrt{6}$的整数有：-2，-1，0，1，2，共5个．
故答案为：5．
点评 此题主要考查了估算无理数的大小，正确得出$\sqrt{6}$的取值范围是解题关键．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
5．下列根式中与$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{3}$ | C． | $\sqrt{6}$ | D． | $\sqrt{18}$ |
2．代数式1-$\frac{{x}^{2}}{x}$是（ ）
| A． | 单项式 | B． | 多项式 | C． | 分式 | D． | 整式 |
19．在下列实数中：$\sqrt{5}$，$\root{3}{π^3}$，3.01001000100001…，$\sqrt{16}$，$\frac{22}{7}$，$\root{3}{-9}$，无理数的个数（ ）个．
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
3．
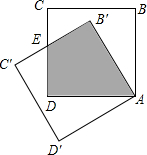如图，边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′，则图中阴影部分面积为（ ）
如图，边长为1的正方形绕点A逆时针旋转30°得正方形AB′C′D′，则图中阴影部分面积为（ ）| A． | 1-$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | 1-$\frac{2\sqrt{3}}{3}$ |
如图，小李周末8时骑自行车从家里出发，到野外郊游，16时回到家里．他离开家后的距离S（千米）与时间t（时）的关系可以用图中的曲线表示．根据这个图象回答下列问题：