题目内容
11.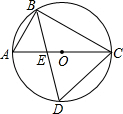 如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°,按以下步骤作图:①以点B为圆心,小于AB的长为半径画弧,分别交AB、BC于点M、N; ②分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧相交于点G;③连结BG交AC边于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比为$\frac{1}{2}$.
如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°,按以下步骤作图:①以点B为圆心,小于AB的长为半径画弧,分别交AB、BC于点M、N; ②分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧相交于点G;③连结BG交AC边于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比为$\frac{1}{2}$.
分析 连接AD.设AB=a,利用勾股定理求出AC、CD,由△EBA∽△ECD推出$\frac{{S}_{△EBA}}{{S}_{△ECD}}$=($\frac{AB}{CD}$)2,由此即可解决问题.
解答 解:如图,连接AD.设AB=a,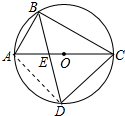
∵AC是直径,
∴∠ABC=∠ADC=90°,
∵∠ACB=30°,
∴AC=2AB=2a,
∵∠DBA=∠DBC,
∴AD=CD,
∵AD2+DC2=AC2,
∴AD=CD=$\sqrt{2}$a,
∵∠EAB=∠EDC,∠EBA=∠ECD,
∴△EBA∽△ECD,
∴$\frac{{S}_{△EBA}}{{S}_{△ECD}}$=($\frac{AB}{CD}$)2=($\frac{a}{\sqrt{2}a}$)2=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题考查基本作图、角平分线的性质.圆的有关知识,解题的关键是利用相似三角形的性质解决问题,学会添加常用辅助线,构造相似三角形,属于中考常考题型.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
1.如图所示,函数y=-x-2的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列各式中,不相等的是( )
| A. | |-2|3和|-23| | B. | (-3)2和32 | C. | (-2)3和-23 | D. | (-3)2和-32 |
20.函数y=$\frac{2}{x}$(y>0)与y=2x(y>0)的交点坐标为( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,2) | D. | (-1,-2) |
 如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.