题目内容
11.在一个不透明的围棋盒子中有x颗白色棋子、y颗黑色棋子,它们除颜色外都一致,从盒子中随机取出一颗棋子,它中黑色棋子的概率为$\frac{2}{3}$;(1)请写出y和x之间的函数关系式;
(2)现在往盒子中再放进5颗白色棋子和1颗黑色棋子,这时随机取出白色棋子的概率为$\frac{1}{2}$,请求出x和y的值.
分析 (1)根据白色棋子的概率得到黑色棋子与白色棋子的数量之比,进而可得y与x的关系;
(2)根据白色棋子的概率得到等量关系,列方程求解即可.
解答 解:(1)由题意得:$\frac{y}{x+y}=\frac{2}{3}$,
∴y与x间的函数关系式为:y=2x;
(2)由题意得:$\left\{\begin{array}{l}\frac{y}{x+y}=\frac{2}{3}\\ \frac{x+5}{x+5+y+1}=\frac{1}{2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=4\\ y=8\end{array}\right.$,
故:x的值为4,y的值为8.
点评 考查概率公式的应用;注意第2步应把5颗白棋子也加入到总棋子数里面.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,则两次摸出的卡片的数字之和等于4的概率( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
3.3-1的值等于( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
1.若α、β是方程x2-4x-5=0的两个实数根,则α2+β2的值为( )
| A. | 30 | B. | 26 | C. | 10 | D. | 6 |

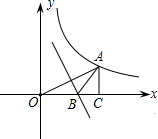 如图,点A(3,m)在双曲线$y=\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( )
如图,点A(3,m)在双曲线$y=\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( )