Question

19．如图1，海边有两个灯塔A，B．即将靠岸的轮船得到信息：海里有一个以AB为弦的弓形暗礁区域，要求轮船在行驶过程中，对两灯塔的张角不能超过45°．当轮船航行到P点时，测得轮船对两灯塔的张角∠APB刚好等于45°．
（1）请用直尺和圆规在图中作出如图2△APB的外接圆（作出图形，不写作法，保留痕迹）；
（2）若此时轮船到B的距离PB为700米，已知AB=500米，求出此时轮船到A的距离．

Answer 1

分析 （1）作任意两边的垂直平分线，交点即为外接圆的圆心；
（2）过B作BH⊥AP，将整个三角形分成两个含有特殊角的三角形求解即可．

解答 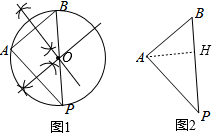解：（1）如图1：⊙O就是所求作的圆．

（2）如图2，过A作AH⊥BP，
在Rt△APH中，
∵∠P=45，
∴AH=PH
设AH=PH=x，则BH=700-x
在Rt△BAH中，x²+（700-x）²=500²，
∴x²-700x+120000=0，
解得：x=300或x=400，
∴AP=$300\sqrt{2}$米或AP=$400\sqrt{2}$米．
答：轮船距离B有$300\sqrt{2}$或$400\sqrt{2}$米．

点评 本题考查了勾股定理及基本作图的知识，解题的关键是将整个三角形分成两个含有特殊角的三角形，难度不大．