题目内容
若方程组
的解(x,y)为整数,求满足条件的质数P.
|
考点:高次方程
专题:
分析:先因式分解x2-y2=(x+y)(x-y),根据P为质数得出①当x+y=1时,x-y=P,②当x+y=P时,x-y=1,分别求出P的值.判定是否满足质数P求解.
解答:解:x2-y2=(x+y)(x-y)=p
∵P为质数,
∴当x+y=1时,x-y=P,
∵3xy+P(x-y)=P2,
∴
[(x+y)2-(x-y)2]+P2=P2,
∴
(1-P2)=0,解得P=±1(舍去P是质数),.
当x+y=P时,x-y=1,
∵3xy+P(x-y)=P2,
∴
[(x+y)2-(x-y)2]+P=P2,
∴
(P2-1)+P=P2,化简得P2-4P+3=0解得P=1或3.
∵P是质数,
∴P=3.
∴满足条件的质数P是3.
∵P为质数,
∴当x+y=1时,x-y=P,
∵3xy+P(x-y)=P2,
∴
| 3 |
| 4 |
∴
| 3 |
| 4 |
当x+y=P时,x-y=1,
∵3xy+P(x-y)=P2,
∴
| 3 |
| 4 |
∴
| 3 |
| 4 |
∵P是质数,
∴P=3.
∴满足条件的质数P是3.
点评:本题主要考查了高次方程,解题的关键是明确质数的定义.

练习册系列答案
相关题目
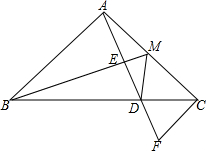 已知如图,在△ABC中,∠BAC=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E,CF⊥AC,证明:
已知如图,在△ABC中,∠BAC=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E,CF⊥AC,证明: