题目内容
△ABC的周长为l6,连接△ABC三边中点构成第一个三角形,再连接这个新三角形的各边中点构成第二个三角形,依此类推,则第2013个三角形的周长为 .
考点:三角形中位线定理
专题:规律型
分析:设△ABC三边AB、BC、CA的中点分别为D、E、F,由三角形中位线定理可分别求得DE+EF+FD,可求得△DEF的周长为△ABC周长的一半,依此类推可求得答案.
解答:
解:设△ABC三边中点分别为D、E、F,
则DE=
AC,EF=
AB,FD=
BC,
∴DE+EF+FD=
(AC+AB+BC)=
×16,
同理,第二次连接各边中点所得第二个三角形的周长为
×
×16,
…
∴第2013个三角形的周长为(
)2013×16=(
)2009,
故答案为:(
)2009.
则DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴DE+EF+FD=
| 1 |
| 2 |
| 1 |
| 2 |
同理,第二次连接各边中点所得第二个三角形的周长为
| 1 |
| 2 |
| 1 |
| 2 |
…
∴第2013个三角形的周长为(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题主要考查三角形中位线定理,根据中位线定理找到每个三角形的周长与△ABC的周长的关系是解题的关键.

练习册系列答案
相关题目
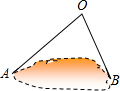 如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )| A、5米 | B、10米 |
| C、15米 | D、20米 |
 下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )
下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )A、 |
B、 |
C、 |
D、 |
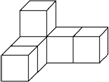 由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )
由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、三个视图的面积一样大 |
 如图,用一个边长为6cm的等边三角形纸片制作一个最大的正六边形,则这个正六边形的边心距是
如图,用一个边长为6cm的等边三角形纸片制作一个最大的正六边形,则这个正六边形的边心距是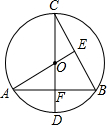 如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2
如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2 如图,AB是⊙O的直径,C、D两点在⊙O上,若∠BAC为28°,则∠ADC=
如图,AB是⊙O的直径,C、D两点在⊙O上,若∠BAC为28°,则∠ADC= 如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=
如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=