题目内容
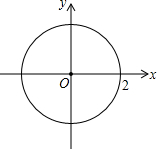 如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.
如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.考点:相切两圆的性质
专题:
分析:如图,首先求出点P在x轴正半轴上时,点P的坐标;进而直接写出点P在坐标轴上的坐标,即可解决问题.
解答:
 解:如图,当圆心P在x轴的正半轴上时,
解:如图,当圆心P在x轴的正半轴上时,
若两圆内切,则OP=2-1=1;若两圆外切,则OP=2+1=3,
∴点P的坐标为P(1,0)或(3,0);
∴当点P在坐标轴上时,满足条件的所有点P的坐标分别为:
(1,0)、(3,0)、(-1,0)、(-3,0)、(0,1)
(0,3)、(0,-1)、(0,-3).
 解:如图,当圆心P在x轴的正半轴上时,
解:如图,当圆心P在x轴的正半轴上时,若两圆内切,则OP=2-1=1;若两圆外切,则OP=2+1=3,
∴点P的坐标为P(1,0)或(3,0);
∴当点P在坐标轴上时,满足条件的所有点P的坐标分别为:
(1,0)、(3,0)、(-1,0)、(-3,0)、(0,1)
(0,3)、(0,-1)、(0,-3).
点评:该题主要考查了相切两圆的性质及其应用问题;牢固掌握相切两圆的性质是灵活运用、解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列各对数中,数值相等的是( )
| A、-2+3与|-2|+|3| | ||
| B、-(-3)与-|-3| | ||
| C、23与32 | ||
D、2÷
|
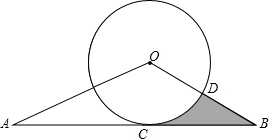 如图,已知△AOB与⊙O相切于点C,边OB与⊙O 相交于点D,OD=BD且SinA=
如图,已知△AOB与⊙O相切于点C,边OB与⊙O 相交于点D,OD=BD且SinA= 某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据: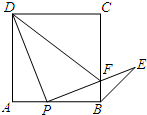 如图,正方形ABCD的边AB上有一点P(不与A、B重合),连接PD并将线段PD绕着点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.则∠CBE的度数是
如图,正方形ABCD的边AB上有一点P(不与A、B重合),连接PD并将线段PD绕着点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.则∠CBE的度数是
 如图,用一个边长为6cm的等边三角形纸片制作一个最大的正六边形,则这个正六边形的边心距是
如图,用一个边长为6cm的等边三角形纸片制作一个最大的正六边形,则这个正六边形的边心距是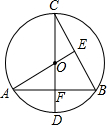 如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2
如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2