题目内容
 如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC,△BCD的周长为13,求BC和ED的长.
如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC,△BCD的周长为13,求BC和ED的长.考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:首先根据线段垂直平分线的性质可得AD=BD,由AC=8可得BD+CD=8,再根据△BCD的周长为13可得BC=13-8=5,进而可得BD=5,再根据勾股定理可得ED的长.
解答:
解:∵DE是AB的垂直平分线,
∴AD=BD,
∵AC=8,
∴BD+CD=8,
∵△BCD的周长为13,
∴BC=13-8=5,
∵BD=BC,
∴BD=5,
∵DE是AB的垂直平分线,
∴BE=4,
∴DE=
=3.
∴AD=BD,
∵AC=8,
∴BD+CD=8,
∵△BCD的周长为13,
∴BC=13-8=5,

∵BD=BC,
∴BD=5,
∵DE是AB的垂直平分线,
∴BE=4,
∴DE=
| 52-42 |
点评:此题主要考查了线段垂直平分线的性质,关键是掌握垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
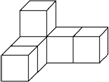 由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )
由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、三个视图的面积一样大 |
已知a、b互为相反数,x、y互为倒数,则5|a+b|-5xy的值是( )
| A、5 | B、-5 | C、10 | D、-10 |
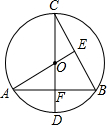 如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2
如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,BC=2 如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=
如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC= 如图,DE∥BC,点D为AB的中点,BC=2
如图,DE∥BC,点D为AB的中点,BC=2