题目内容
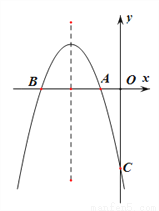
如图,已知抛物线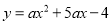 交
交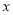 轴于点
轴于点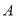 、点
、点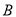 ,交
,交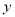 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求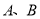 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点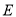 异于
异于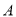 ,且
,且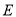 在对称轴右侧),直线
在对称轴右侧),直线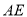 交对称轴于N,
交对称轴于N,
直线BE交对称轴于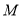 ,对称轴交
,对称轴交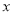 轴于
轴于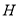 ,试确定
,试确定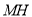 、
、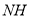 的数量关系并说明理由.
的数量关系并说明理由.
练习册系列答案
相关题目
题目内容
如图,已知抛物线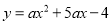 交
交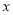 轴于点
轴于点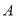 、点
、点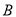 ,交
,交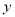 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求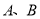 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点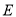 异于
异于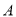 ,且
,且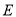 在对称轴右侧),直线
在对称轴右侧),直线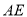 交对称轴于N,
交对称轴于N,
直线BE交对称轴于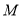 ,对称轴交
,对称轴交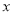 轴于
轴于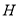 ,试确定
,试确定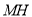 、
、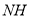 的数量关系并说明理由.
的数量关系并说明理由.
