题目内容
17.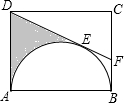 矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=$\sqrt{3}$,则阴影部分的面积为9$\sqrt{3}$-3π.
矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=$\sqrt{3}$,则阴影部分的面积为9$\sqrt{3}$-3π.
分析 连接OF、OE、OD,如图,在Rt△OBF中利用三角函数的定义求出∠OFB=60°,再利用切线的性质和切线长定理得到∠OFE=∠OFB=60°,OE⊥DF,所以∠BFE=120°,则∠ADE=60°,同样可得∠ADO=∠EDO=30°,利用含30度的直角三角形三边的关系求出AD=$\sqrt{3}$OA=3$\sqrt{3}$,所以S△ADO=$\frac{9\sqrt{3}}{2}$;接着计算出∠AOE=120°,于是得到S扇形AO=3π,然后利用阴影部分的面积=四边形AOED的面积-扇形AOE的面积进行计算即可.
解答 解:连接OF、OE、OD,如图,
在Rt△OBF中,∵tan∠OFB=$\frac{OB}{BF}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴∠OFB=60°,
∵BF⊥AB,
∴BF为切线,
∵DF为切线,
∴∠OFE=∠OFB=60°,OE⊥DF,
∴∠BFE=120°,
∵BC∥AD,
∴∠ADE=60°,
∵AD⊥AB,
∴AD为切线,
而DE为切线,
∴∠ADO=∠EDO=30°,
在Rt△AOD中,AD=$\sqrt{3}$OA=3$\sqrt{3}$,
∴S△ADO=$\frac{1}{2}$×3×3$\sqrt{3}$=$\frac{9\sqrt{3}}{2}$;
∵∠AOE=180°-∠ADE=120°,
∴S扇形AOE=$\frac{120•π•{3}^{2}}{360}$=3π,
∴阴影部分的面积=四边形AOED的面积-扇形AOE的面积=2×$\frac{9\sqrt{3}}{2}$-3π=9$\sqrt{3}$-3π.
故答案为9$\sqrt{3}$-3π.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理.

| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 生产量与计划量的差值 | +5 | -2 | -4 | +13 | -10 | +14 | -9 |
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产多少辆自行车?
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
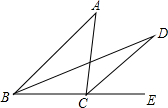 如图,在△ABC中,∠A=40°,BD,CD分别是∠ABC与外角∠ACE的平分线,并交于点D,则∠D的度数为20°.
如图,在△ABC中,∠A=40°,BD,CD分别是∠ABC与外角∠ACE的平分线,并交于点D,则∠D的度数为20°.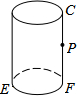 如图:有一个圆柱,底面圆的直径EF=$\frac{16}{π}$,高FC=12cm,P为FC的中点,求蚂蚁从E点爬到P点的最短距离是多少?(画出平面图形)
如图:有一个圆柱,底面圆的直径EF=$\frac{16}{π}$,高FC=12cm,P为FC的中点,求蚂蚁从E点爬到P点的最短距离是多少?(画出平面图形)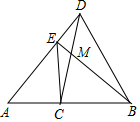 如图,已知点C为线段AB的中点,以BC为边作△DBC,使DC=DB,连接AD,过点C作CE⊥AB交AD于点E,连接BE交CD于点M.
如图,已知点C为线段AB的中点,以BC为边作△DBC,使DC=DB,连接AD,过点C作CE⊥AB交AD于点E,连接BE交CD于点M.