题目内容
13．已知x，y，z为有理数，A=2x3-xyz，B=3y2-z2+xyz，C=x3+2y2-xyz，且（x+1）2+（y-1）2+|z|=0，求A-[2B-3（C-A）]的值．分析 利用非负数的性质求出x，y，z的值，原式去括号合并后代入计算即可求出值．
解答 解：∵（x+1）2+（y-1）2+|z|=0，
∴x=-1，y=1，z=0，
则原式=A-2B+3C-3A=-2A-2B+3C=-2（2x3-xyz）-2（3y2-z2+xyz）+3（x3+2y2-xyz）=-4x3+2xyz-6y2+2z2-2xyz+3x3+6y2-3xyz=-x3+2z2-3xyz=1+0-0=1．
点评 此题考查了整式的加减-化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
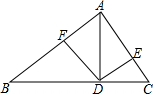如图，∠BAC=90°，AD⊥BC，DE⊥AC，DF⊥AB，∠B=30°，则图中有8对线段其中一条是另一条的一半．