题目内容
3.若$\sqrt{x-2y+9}$与|x-y+3|互为相反数,则x+y的值为( )| A. | 3 | B. | 9 | C. | 12 | D. | 27 |
分析 利用互为相反数两数之和为0列出关系式,再利用非负数的性质得出方程组,求出方程组的解得到x与y的值,即可求出x+y的值.
解答 解:由题意得:$\sqrt{x-2y+9}$+|x-y+3|=0,
可得$\left\{\begin{array}{l}{x-2y=-9①}\\{x-y=-3②}\end{array}\right.$,
②-①得:y=6,
把y=6代入②得:x=3,
则x+y=9,
故选B
点评 此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.某省2013年的快递业务量为1.5亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展.若2015年的快递业务量达到4.5亿件.设2014年与2013年这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.5(1+x)=4.5 | B. | 1.5(1+2x)=4.5 | ||
| C. | 1.5(1+x)2=4.5 | D. | 1.5(1+x)+1.4(1+x)2=4.5 |
11.以a,b,c为边长的下列三角形,能判定是直角三角形的有( )
①a:b:c=1:1:$\sqrt{2}$;
②a,b,c满足a2-b2=c2;
③a=m2+n2,b=mn,c=m2-n2(m>n>0);
④a=1,b=2,c=$\sqrt{3}$.
①a:b:c=1:1:$\sqrt{2}$;
②a,b,c满足a2-b2=c2;
③a=m2+n2,b=mn,c=m2-n2(m>n>0);
④a=1,b=2,c=$\sqrt{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.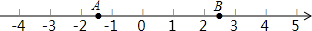 如图,数轴上两点A、B表示的数可能是( )
如图,数轴上两点A、B表示的数可能是( )
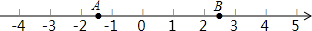 如图,数轴上两点A、B表示的数可能是( )
如图,数轴上两点A、B表示的数可能是( )| A. | -1.5和2.5 | B. | -2.5和2.5 | C. | -1.5和3.5 | D. | -2.5和3.5 |
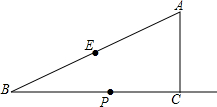 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.
 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.