题目内容
18.解方程组:$\left\{\begin{array}{l}{{x}^{2}+6xy+9{y}^{2}=9}\\{{x}^{2}-{y}^{2}-4x+4y=0}\end{array}\right.$.分析 先把方程组的两个方程变形,即可得出四个二元一次方程组,求出每个方程组的解即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+6xy+9{y}^{2}=9①}\\{{x}^{2}-{y}^{2}-4x+4y=0②}\end{array}\right.$
由①得:(x+y)2=9,
x+y=±3③,
由②得:(x+y)(x-y)-4(x-y)=0,
x-y=0,x+y-4=0,
即原方程组化为四个方程组:Ⅰ、$\left\{\begin{array}{l}{x+y=3}\\{x-y=0}\end{array}\right.$、Ⅱ、$\left\{\begin{array}{l}{x+y=3}\\{x+y-4=0}\end{array}\right.$,Ⅲ、$\left\{\begin{array}{l}{x+y=-3}\\{x-y=0}\end{array}\right.$,Ⅳ、$\left\{\begin{array}{l}{x+y=-3}\\{x+y-4=0}\end{array}\right.$
解得:方程组组Ⅰ的解为$\left\{\begin{array}{l}{x=1.5}\\{y=1.5}\end{array}\right.$,方程组Ⅱ无解,方程组Ⅲ的解为$\left\{\begin{array}{l}{x=-1.5}\\{y=-1.5}\end{array}\right.$,方程组Ⅳ无解,
所以原方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=1.5}\\{{y}_{1}=1.5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1.5}\\{{y}_{2}=-1.5}\end{array}\right.$.
点评 本题考查了解高次方程组的应用,能把高次方程组转化成二元一次方程组是解此题的关键.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的童装?并说明理由.
| 甲种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 15 | 30 | 15 | |
| 乙种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 30 | 15 | 30 |
| A. | 3 | B. | 9 | C. | 12 | D. | 27 |
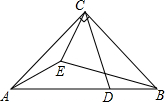 如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.