Question

4．某单位有一块四边形的空地，∠B=90°，量得各边的长度如图（单位：米）．现计划在空地内种草，若每平方米草地造价30元，这块地全部种草的费用是多少元？

Answer 1

分析 连接AC，先证明△ACD是直角三角形，根据S_{四边形ABCD}=S_△BAC+S_△DAC求出四边形ABCD的面积即可解决问题．

解答 解：连接AC，
∵∠B=90°，
∴在Rt△ABC中，AC²=AB²+BC=3²+4²=5²，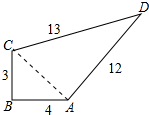
在△ACD中，CD²=13²，AD²=12²，
∵5²+12²=13²，
∴AC²+AD²=CD²，
∴∠DAC=90°，
∴S_{四边形ABCD}=S_△BAC+S_△DAC=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AC•AD=36cm²，
∵36×30=1080（元），
∴这块地全部种草的费用是1080元

点评 本题考查勾股定理以及勾股定理的逆定理的应用，解题的关键是证明△ADC是直角三角形，属于中考常考题型．