题目内容
4. 如图所示,将长方形ABCD的纸片沿EF折叠,点D、C分别落在点D′、C′处,若∠AED′=50°,则∠EFB的度数为65°.
如图所示,将长方形ABCD的纸片沿EF折叠,点D、C分别落在点D′、C′处,若∠AED′=50°,则∠EFB的度数为65°.
分析 根据平角的定义可得∠DED′的度数,再由折叠的性质可得∠D′EF=∠DEF=$\frac{1}{2}$∠DED′,根据平行线的性质可得出∠EFB的度数.
解答 解:∵∠AED′=50°,
∴∠DED′=180°-50°=130°,
由折叠的性质可得,∠D′EF=∠DEF=$\frac{1}{2}$∠DED′=65°,
又∵AD∥BC,
∴∠EFB=∠DEF=65°.
故答案为:65°.
点评 此题考查了平行线的性质以及翻折变换的运用,解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=$\frac{1}{2}$∠DED′,注意两直线平行,内错角相等的灵活运用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
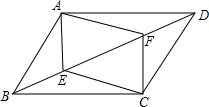 如图:在?ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.
如图:在?ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.
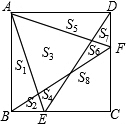 如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…S8,若S2=2,S7=3,S8=8,则S3的值为13.
如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…S8,若S2=2,S7=3,S8=8,则S3的值为13.