题目内容
14.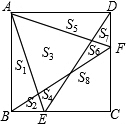 如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…S8,若S2=2,S7=3,S8=8,则S3的值为13.
如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…S8,若S2=2,S7=3,S8=8,则S3的值为13.
分析 根据图示可知,S3=SABCD-S△ABE-S△BCF-S△CDE-S△ADF+S2+S7+S8,只要证明S3=S2+S7+S8即可解决问题.
解答 解:由题意S3=SABCD-S△ABE-S△BCF-S△CDE-S△ADF+S2+S7+S8,
化简得S3=BC•CD-$\frac{1}{2}$×(BE+EC)×CD-$\frac{1}{2}$×(DF+FC)×BC+S2+S7+S8,
∵四边形ABCD是正方形,
∴BC=CD,
∴BC•CD=$\frac{1}{2}$×(BE+EC)×CD+$\frac{1}{2}$×(DF+FC),
∴S3=S2+S7+S8=2+3+8=13.
故答案为13.
点评 本题考查了正方形的性质,三角形的面积等知识,解题的关键是证明S3=S2+S7+S8,学会用分割法求多边形的面积.

练习册系列答案
相关题目
9.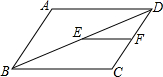 如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
 如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | 8 | D. | 9 |
6.若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是( )
| A. | -9 | B. | -3 | C. | 3 | D. | -3或3 |
 如图所示,将长方形ABCD的纸片沿EF折叠,点D、C分别落在点D′、C′处,若∠AED′=50°,则∠EFB的度数为65°.
如图所示,将长方形ABCD的纸片沿EF折叠,点D、C分别落在点D′、C′处,若∠AED′=50°,则∠EFB的度数为65°.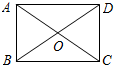 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是2$\sqrt{3}$.
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是2$\sqrt{3}$.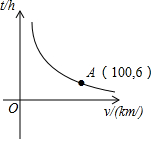 一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h)
一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h) 已知线段AB=8,延长AB到C,使BC=6.如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?(自己将图补充完整并请写出求解过程)
已知线段AB=8,延长AB到C,使BC=6.如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?(自己将图补充完整并请写出求解过程)