题目内容
13.有一天李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.(1)你能探究出图一到图四各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
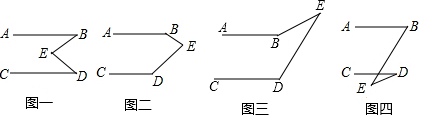
分析 (1)根据各角的不同位置,即可得到各角之间的数量关系;
(2)通过作辅助线,构造内错角,同位角以及同旁内角,依据平行线的性质以及三角形外角性质进行计算即可.
解答 解:(1)∠B,∠D与∠BED之间的关系分别是:①∠B+∠D=∠BED;②∠B+∠D+∠BED=360°;③∠B=∠BED+∠D;④∠B=∠D+∠BED;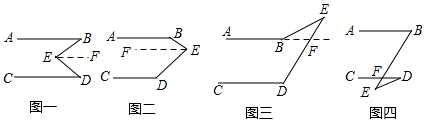
(2)选择①.
过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D;
选择②.
过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF=180°,∠D+∠DEF=180°,
∴∠D+∠BED+∠D=180°+180°=360°;
选择③.
延长AB交DE于F,
∵AB∥CD,
∴∠D=∠BFE,
∵∠ABE是△BEF的外角,
∴∠ABE=∠E+∠BFE=∠E+∠D;
选择④.
设CD与BE交于点F,
∵AB∥CD,
∴∠B=∠CFE,
∵∠CFE是△DEF的外角,
∴∠CFE=∠D+∠E,即∠B=∠D+∠E.
点评 本题主要考查了平行线的性质的运用,解决问题的关键是作辅助线构造内错角,同位角以及同旁内角,依据两直线平行,内错角相等,同位角相等以及同旁内角互补进行计算.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.某商场销售A、B两种商品,这两种商品的进价和售价如表所示,该商场计划购进两种商品若干,共需66万元,全部销售后可获利润9万元.
(1)该商场计划购进A、B两种商品各多少件?;
(2)通过市场调研,该商场决定在原计划的基础上,减少A种商品的购进数量,增加B种商品的购进数量,已知B种商品增加的数量是A种商品减少的数量的1.5倍.若用于购进这两种商品的总资金不超过69万.问A种商品购进数至多减少多少件?
| A | B | |
| 进价(万元/件) | 1.5 | 1.2 |
| 售价(万元/件) | 1.65 | 1.4 |
(2)通过市场调研,该商场决定在原计划的基础上,减少A种商品的购进数量,增加B种商品的购进数量,已知B种商品增加的数量是A种商品减少的数量的1.5倍.若用于购进这两种商品的总资金不超过69万.问A种商品购进数至多减少多少件?
18.下列方程中关于x的一元二次方程的是( )
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | ax2+bx+c=0 |
 如图所示,将长方形ABCD的纸片沿EF折叠,点D、C分别落在点D′、C′处,若∠AED′=50°,则∠EFB的度数为65°.
如图所示,将长方形ABCD的纸片沿EF折叠,点D、C分别落在点D′、C′处,若∠AED′=50°,则∠EFB的度数为65°.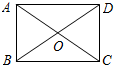 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是2$\sqrt{3}$.
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是2$\sqrt{3}$.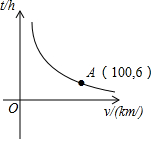 一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h)
一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h)