题目内容
如图1的图形,像我们常见的风筝.我们不妨把这样图形叫做“筝形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?
下面就请你发挥你的聪明才智,解决以下问题:
观察“筝形”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
请你直接利用以上结论,解决以下三个问题:
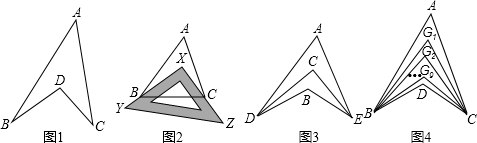
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=58°,则∠ABX+∠ACX= °;
②如图3,已知DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=150°,则∠DCE= °;
②如图4,已知∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠B G1C=77°,则∠A= °.
下面就请你发挥你的聪明才智,解决以下问题:
观察“筝形”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
请你直接利用以上结论,解决以下三个问题:

①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=58°,则∠ABX+∠ACX=
②如图3,已知DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=150°,则∠DCE=
②如图4,已知∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠B G1C=77°,则∠A=
考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:根据三角形外角性质得∠3=∠B+∠1,∠4=∠2+∠C,然后把两式相加即可得到∠BDC=∠A+∠B+∠C;
①由前面的结论得∠BXC=∠A+∠ABX+∠ACX,所以∠ABX+∠ACX=90°-58°=32°;
②由前面的结论得到∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,再根据角平分线的定义得∠ADC=∠BDC,∠ACE=∠BEC,所以∠DBE-∠DCE=∠DCE-∠A,然后把∠DAE=60°,∠DBE=150°代入计算即可;
③由前面的结论得∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,则∠ABG1=
∠ABD,∠ACG1=
∠ACD,所以10∠BG1C=10∠A+∠ABD+∠ACD,利用等式的性质得到10∠BG1C-∠BDC=9∠A,即有∠A=
(10×77°-140°)=70°.
①由前面的结论得∠BXC=∠A+∠ABX+∠ACX,所以∠ABX+∠ACX=90°-58°=32°;
②由前面的结论得到∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,再根据角平分线的定义得∠ADC=∠BDC,∠ACE=∠BEC,所以∠DBE-∠DCE=∠DCE-∠A,然后把∠DAE=60°,∠DBE=150°代入计算即可;
③由前面的结论得∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,则∠ABG1=
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 9 |
解答: 解:∠BDC=∠A+∠B+∠C.理由如下:
解:∠BDC=∠A+∠B+∠C.理由如下:
作射线AD,如图,
∵∠3=∠B+∠1,∠4=∠2+∠C,
∴∠3+∠4=∠1+∠2+∠B+∠C,
即∠BDC=∠A+∠B+∠C;
①∵∠BXC=∠A+∠ABX+∠ACX,
∴∠ABX+∠ACX=90°-58°=32°;
②∵∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠BDC,∠ACE=∠BEC,
∴∠DBE-∠DCE=∠DCE-∠A,
∴∠DCE=
(∠DBE+∠A)=
×(150°+60°)=105°;
③∵∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,
而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,
∴∠ABG1=
∠ABD,∠ACG1=
∠ACD,
∴10∠BG1C=10∠A+∠ABD+∠ACD,
∴10∠BG1C-∠BDC=9∠A,
∴∠A=
(10×77°-140°)=70°.
故答案为32,105,70.
 解:∠BDC=∠A+∠B+∠C.理由如下:
解:∠BDC=∠A+∠B+∠C.理由如下:作射线AD,如图,
∵∠3=∠B+∠1,∠4=∠2+∠C,
∴∠3+∠4=∠1+∠2+∠B+∠C,
即∠BDC=∠A+∠B+∠C;
①∵∠BXC=∠A+∠ABX+∠ACX,
∴∠ABX+∠ACX=90°-58°=32°;
②∵∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠BDC,∠ACE=∠BEC,
∴∠DBE-∠DCE=∠DCE-∠A,
∴∠DCE=
| 1 |
| 2 |
| 1 |
| 2 |
③∵∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,
而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,
∴∠ABG1=
| 1 |
| 10 |
| 1 |
| 10 |
∴10∠BG1C=10∠A+∠ABD+∠ACD,
∴10∠BG1C-∠BDC=9∠A,
∴∠A=
| 1 |
| 9 |
故答案为32,105,70.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线的定义和三角形外角性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为 (1)计算:(2013-π)0+4sin60°-
(1)计算:(2013-π)0+4sin60°-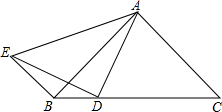 △ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.
△ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB. 如图,AC⊥AB于A,BD⊥AB于B,AC=10,BD=6,O为CD的中点,过O作OM⊥AB于M,求OM的长.
如图,AC⊥AB于A,BD⊥AB于B,AC=10,BD=6,O为CD的中点,过O作OM⊥AB于M,求OM的长. 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠BAC的度数是
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠BAC的度数是