题目内容
9.已知:如图,在△ABC和△A′B′C′,∠ACB=∠A′C′B′=Rt∠,CD、C′D′分别是△ABC和△A′B′C′的中线,且CD=C′D′,CE、C′E′分别是△ABC和△A′B′C′的高线,且CE=C′E′,求证:Rt△ABC≌Rt△A′B′C′.
分析 证明△CED与△C'E'D'全等,得出∠B=∠B',∠CDB=∠C'D'B',再证明△CDB与△C'D'B'全等,得出BC=B'C',进而证明即可.
解答 证明:在Rt△CED与Rt△C'E'D'中,
$\left\{\begin{array}{l}{CE=C'E'}\\{CD=C'D'}\end{array}\right.$,
∴Rt△CED≌Rt△C'E'D'(HL),
∴∠CDE=∠C'D'E'',
∵CD=DB,C'D'=D'B',
∴∠B=∠B',∠CDB=∠C'D'B',
在△CDB与△C'D'B'中,
$\left\{\begin{array}{l}{∠B=∠B'}\\{∠CDB=∠C'D'B'}\\{CD=C'D'}\end{array}\right.$,
∴△CDB≌△C'D'B'(AAS),
∴BC=B'C',∠B=∠B',
在Rt△ABC与Rt△A′B′C′中,
$\left\{\begin{array}{l}{∠ACB=∠A'C'B'}\\{BC=B'C'}\\{∠B=∠B'}\end{array}\right.$,
∴Rt△ABC≌Rt△A′B′C′(ASA).
点评 此题考查全等三角形的判定,关键是证明△CED与△C'E'D'全等,得出∠B=∠B',∠CDB=∠C'D'B'.

练习册系列答案
相关题目
1.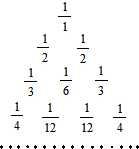 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )
 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第2个数(从左到右)为( )| A. | $\frac{1}{56}$ | B. | $\frac{1}{60}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{168}$ |
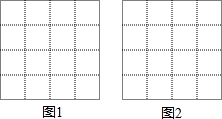 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图: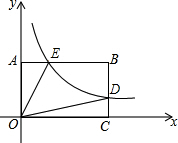 如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.
如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.