题目内容
9．$\sqrt{5}$是一个无理数，请估计$\sqrt{5}$在哪两个整数之间？（ ）| A． | 1与2 | B． | 2与3 | C． | 3与4 | D． | 4与5 |
分析 由于4＜5＜9，然后利用算术平方根即可得到2＜$\sqrt{5}$＜3．
解答 解：∵4＜5＜9，
∴2＜$\sqrt{5}$＜3．
故选B．
点评 本题考查了估算无理数的大小：利用完全平方数和算术平方根对无理数的大小进行估算．
练习册系列答案
相关题目
19．
如图，点O在直线AB上，点M，N在直线AB外，若MO⊥AB，NO⊥AB，垂足均为O，则可得点N在直线MO上，其理由是（ ）
如图，点O在直线AB上，点M，N在直线AB外，若MO⊥AB，NO⊥AB，垂足均为O，则可得点N在直线MO上，其理由是（ ）| A． | 经过两点有且只有一条直线 | |
| B． | 在一平面上，一条直线只有一条垂线 | |
| C． | 垂线段最短 | |
| D． | 在同一平面内，过一点有且只有一条直线与已知直线垂直 |
20．下列各组二次根式中是同类二次根式的是（ ）
| A． | $\sqrt{6}与\sqrt{24}$ | B． | $\sqrt{18}与\sqrt{\frac{1}{3}}$ | C． | $\sqrt{2}与\sqrt{12}$ | D． | $\sqrt{0.2}与\sqrt{27}$ |
4．在数轴上，一个点从-3开始向左移动1个单位长度，再向右移动2个单位长度得到点B，则点B表示的数是（ ）
| A． | +3 | B． | +1 | C． | -9 | D． | -2 |
14．已知a、b满足$\sqrt{a-\frac{1}{4}}$+|2b+1|=0，则$\sqrt{a}$+b的值是（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | -1 | D． | 0 |
19．
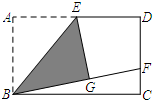如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=2，FD=4，则BC的长为（ ）
如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=2，FD=4，则BC的长为（ ）| A． | 6$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{5}$ | D． | 4$\sqrt{6}$ |