题目内容
20.下列各组二次根式中是同类二次根式的是( )| A. | $\sqrt{6}与\sqrt{24}$ | B. | $\sqrt{18}与\sqrt{\frac{1}{3}}$ | C. | $\sqrt{2}与\sqrt{12}$ | D. | $\sqrt{0.2}与\sqrt{27}$ |
分析 先把各选项中的二次根式化为最简二次根式,然后根据同类二次根式的定义进行判断.
解答 解:A、$\sqrt{24}$=2$\sqrt{6}$,则$\sqrt{6}$与$\sqrt{24}$为同类二次根式,所以A选项正确;
B、$\sqrt{18}$=3$\sqrt{2}$,$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$,则$\sqrt{18}$与$\sqrt{\frac{1}{3}}$不是同类二次根式,所以B选项错误;
C、$\sqrt{12}$=2$\sqrt{3}$,则$\sqrt{2}$与$\sqrt{12}$不是同类二次根式,所以C选项错误;
D、$\sqrt{0.2}$=$\frac{\sqrt{5}}{5}$,$\sqrt{27}$=3$\sqrt{3}$,则$\sqrt{0.2}$与$\sqrt{27}$不是同类二次根式,所以D选项错误.
故选A.
点评 本题考查了同类二次根式:一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.合并同类二次根式的方法:只合并根式外的因式,即系数相加减,被开方数和根指数不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,AB是半圆O的直径,D是$\widehat{AC}$的中点,若∠BAC=40°,则∠DAC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$的中点,若∠BAC=40°,则∠DAC的度数是( )
 如图,AB是半圆O的直径,D是$\widehat{AC}$的中点,若∠BAC=40°,则∠DAC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$的中点,若∠BAC=40°,则∠DAC的度数是( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
15.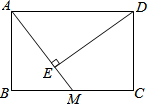 如图,在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
 如图,在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\frac{5}{2}$,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )| A. | 1 | B. | $\frac{3\sqrt{13}}{13}$ | C. | $\frac{10\sqrt{41}}{41}$ | D. | $\frac{\sqrt{41}}{10}$ |
12.下列不是具有相反意义的量是( )
| A. | 前进5米和后退5米 | B. | 收入10元和支出10元 | ||
| C. | 身高增加2厘米和体重减少2千克 | D. | 超过5克和不足2克 |
9.$\sqrt{5}$是一个无理数,请估计$\sqrt{5}$在哪两个整数之间?( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
