题目内容
 等腰△ABC的腰长AB=10cm,BC=7cm,∠A=50°;DE为腰AB的垂直平分线.①求△BCD的周长;②求∠CBD的度数.
等腰△ABC的腰长AB=10cm,BC=7cm,∠A=50°;DE为腰AB的垂直平分线.①求△BCD的周长;②求∠CBD的度数.考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:①利用线段垂直平分线的性质:垂直平分线上任意一点,和线段两端点的距离相等可解.
②已知∠A=50°,易求∠ABC的度数.又因为DE垂直平分AB根据线段垂直平分线的性质易求出∠CBD的度数.
②已知∠A=50°,易求∠ABC的度数.又因为DE垂直平分AB根据线段垂直平分线的性质易求出∠CBD的度数.
解答:解:①∵DE是AB的垂直平分线,
∴BD=AD,
∴△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC,
即:△BCD的周长=AC+BC.
∵等腰△ABC的腰长AB=10cm,BC=7cm,
∴△BCD的周长=10+7=17(cm).
②∵∠A=50°,
∴∠ABC=∠C=65°,
又∵DE垂直平分AB,
∴∠A=∠ABD=50°,
∴∠CBD=∠ABC-∠ABD=15°.
∴BD=AD,
∴△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC,
即:△BCD的周长=AC+BC.
∵等腰△ABC的腰长AB=10cm,BC=7cm,
∴△BCD的周长=10+7=17(cm).
②∵∠A=50°,
∴∠ABC=∠C=65°,
又∵DE垂直平分AB,
∴∠A=∠ABD=50°,
∴∠CBD=∠ABC-∠ABD=15°.
点评:本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)有关知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列式子正确的是( )
| A、(-0.2)-2=25 | ||||
B、(-
| ||||
| C、(-2)-3=-8 | ||||
D、(-
|
 在平面直角坐标系中,描出下列各点:A(1,1),B(5,1),C(3,3),D(-3,3),E(-2,2),F(-2,-4),G(5,0),H(3,-4),I(-1,-4),J(3,-2).
在平面直角坐标系中,描出下列各点:A(1,1),B(5,1),C(3,3),D(-3,3),E(-2,2),F(-2,-4),G(5,0),H(3,-4),I(-1,-4),J(3,-2). 在下列所给的三幅图案中再添画一个小正方形,使得每一个所构成的新图案都是轴对称图形.
在下列所给的三幅图案中再添画一个小正方形,使得每一个所构成的新图案都是轴对称图形. 小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图.试分别求出五次成绩的极差和方差.
小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图.试分别求出五次成绩的极差和方差.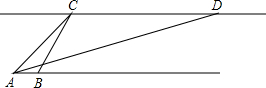 有全国最佳深水岸线资源的宁波拥有丰富的海洋资源,为了科学利用海洋资源,发展海洋经济.市政府对A,B两岛屿的海洋资源进行了可持续开发研究.用某勘测飞机测量两岛屿A,B之间的距离.飞机在高空点C处测得岛屿A的俯角∠ECA为45°,岛屿B的俯角∠ECB为60°,然后沿着平行于AB的方向水平飞行了1200海里到点D处,在点D处测得岛屿A的俯角∠EDA为30°,请你根据以上数据,解决下面两个问题:
有全国最佳深水岸线资源的宁波拥有丰富的海洋资源,为了科学利用海洋资源,发展海洋经济.市政府对A,B两岛屿的海洋资源进行了可持续开发研究.用某勘测飞机测量两岛屿A,B之间的距离.飞机在高空点C处测得岛屿A的俯角∠ECA为45°,岛屿B的俯角∠ECB为60°,然后沿着平行于AB的方向水平飞行了1200海里到点D处,在点D处测得岛屿A的俯角∠EDA为30°,请你根据以上数据,解决下面两个问题: