题目内容
15.若x-y-z=7,x2+y2+z2=15,xyz=6,则$\frac{1}{x}$-$\frac{1}{y}$-$\frac{1}{z}$的值为$\frac{17}{6}$.分析 把x-y-z=7两边平方,利用完全平方公式展开,将x2+y2+z2=15代入求出yz-xz-xy的值,原式变形后代入计算即可求出值.
解答 解:∵x-y-z=7,
∴(x-y-z)2=x2+y2+z2-2xy-2xz+2yz=x2+y2+z2+2(-xy-xz+yz)=49,
∵x2+y2+z2=15,
∴2(yz-xz-xy)=49-15=34,
∴yz-xz-xy=17,
则$\frac{1}{x}$-$\frac{1}{y}$-$\frac{1}{z}$=$\frac{yz-xz-xy}{xyz}$=$\frac{17}{6}$.
故答案为:$\frac{17}{6}$
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.若分式方程$\frac{m-x}{x-3}$=$\frac{1}{3-x}$-3有增根,则m的值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
20.式子|x-2|+|x-6|的最小值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
7.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x-y=m}\\{x+3y=m}\end{array}\right.$(m≠0),则x:y等于( )
| A. | 3:1 | B. | 1:3 | C. | 2:1 | D. | 1:2 |
5.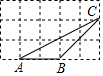 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
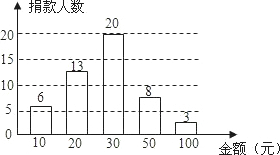 某校九年级(1)班50名学生积极参加献爱心慈善捐款活动,班长将捐款情况进行统计,并绘制成了如图所示的统计图,根据统计图提供的信息,捐款金额中位数是( )
某校九年级(1)班50名学生积极参加献爱心慈善捐款活动,班长将捐款情况进行统计,并绘制成了如图所示的统计图,根据统计图提供的信息,捐款金额中位数是( )