题目内容
6.用公式法解下列方程:(1)x2-6x-16=0
(2)(2x+1)(2x-1)=2$\sqrt{2}$x:
分析 (1)根据公式法的解答方法可以解答此方程;
(2)根据公式法的解答方法可以解答此方程.
解答 解:(1)x2-6x-16=0
∵a=1,b=-6,c=-16,
∴△=(-6)2-4×1×(-16)=100>0,
∴x=$\frac{6±\sqrt{100}}{2×1}=\frac{6±10}{2}$=3±5,
∴x1=-2,x2=8;
(2)(2x+1)(2x-1)=2$\sqrt{2}$x
化简,得
$4{x}^{2}-2\sqrt{2}x-1$=0,
∵a=4,b=-2$\sqrt{2}$,c=-1,
∴$△=(-2\sqrt{2})^{2}-4×4×(-1)=24>0$,
∴x=$\frac{2\sqrt{2}±\sqrt{24}}{2×4}=\frac{2\sqrt{2}±2\sqrt{6}}{8}=\frac{\sqrt{2}±\sqrt{6}}{4}$,
∴x1=$\frac{\sqrt{2}-\sqrt{6}}{4}$,x2=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
点评 本题考查解一元二次方程-公式法,解答本题的关键是明确公式法的解答方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
16. 如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
 如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )| A. | (1,-1) | B. | (2,0) | C. | (-1,1) | D. | (-1,-1) |
1.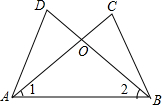 如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需添加条件( )
如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需添加条件( )
 如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需添加条件( )
如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需添加条件( )| A. | ∠D=∠C | B. | OA=OB | C. | AD=BC | D. | AC=BD |
10.将7个数按从小到大顺序排列,去掉最小和最大的两个数后,下列量不发生改变的是( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
 如图所示,AD∥BC,点O在AD上,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=m°,则∠BOC=$\frac{1}{2}$m°.
如图所示,AD∥BC,点O在AD上,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=m°,则∠BOC=$\frac{1}{2}$m°.