题目内容
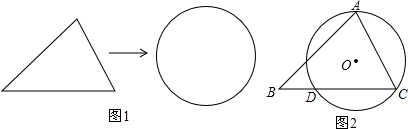
19.某住宅小区将现有一块三角形的绿化地改造为一块圆形的绿化地如图1.已知原来三角形绿化地中道路AB长为16$\sqrt{2}$米,在点B的拐弯处道路AB与BC所夹的∠B为45°,在点C的拐弯处道路AC与BC所夹的∠C的正切值为2(即tan∠C=2),如图2.(1)求拐弯点B与C之间的距离;
(2)在改造好的圆形(圆O)绿化地中,这个圆O过点A、C,并与原道路BC交于点D,如果点A是圆弧(优弧)道路DC的中点,求圆O的半径长.
分析 (1)作AE⊥BC于E,根据正弦函数求得AE,根据等腰直角三角形的性质求得BE,根据正切函数求得EC,进而即可求得BC;
(2)连接AD,先根据已知求得三角形ADC是等腰三角形,进而根据垂径定理的推论求得AE经过圆心,连接OC,根据勾股定理即可求得圆的半径.
解答  解:(1)作AE⊥BC于E,
解:(1)作AE⊥BC于E,
∵∠B=45°,
∴AE=AB•sin45°=16$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=16,
∴BE=AE=16,
∵tan∠C=2,
∴$\frac{AE}{EC}$=2,
∴EC=$\frac{AE}{2}$=8,
∴BC=BE+EC=16+8=24;
(2)连接AD,
∵点A是圆弧(优弧)道路DC的中点,
∴∠ADC=∠C,
∴AD=AC,
∴AE垂直平分DC,
∴AE经过圆心,
设圆O的半径为r,
∴OE=16-r,
在RT△OEC中,OE2+EC2=OC2,
即(16-r)2+82=r2,
解得r=10,
∴圆O的半径为10.
点评 本题考查了解直角三角形的应用,这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.

练习册系列答案
相关题目
9.一组互不相同的数据3、4、6、7、x的中位数是x,若这组数据都是整数,这组数据中的x是( )
| A. | 4 | B. | 6 | C. | 5 | D. | 8 |
8.若点A在第二象限,且到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
| A. | (-3,2) | B. | (3,-2) | C. | (-2,3) | D. | (2,-3) |
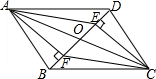 如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.
如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.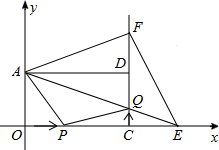 如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2$\sqrt{5}$.
如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2$\sqrt{5}$.