题目内容
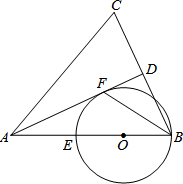 已知:如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.
已知:如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.(1)求证:AD与⊙O相切;
(2)当BC=4,cos∠C=
| 1 |
| 3 |
考点:切线的判定
专题:
分析:(1)如图,作辅助线;证明OF∥BD,根据BD⊥AD,得到OF⊥AD,即可解决问题.
(2)如图,根据题意求出AB、BD的长度;运用△AOF∽△ABD,列出比例式
=
,即
=
,求出λ即可解决问题.
(2)如图,根据题意求出AB、BD的长度;运用△AOF∽△ABD,列出比例式
| OF |
| BD |
| AO |
| AB |
| λ |
| 2 |
| 6-λ |
| 6 |
解答: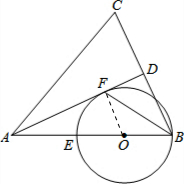 (1)证明:如图,连接OF;
(1)证明:如图,连接OF;
∵OB=OF,
∴∠OFB=∠OBF,而BF平分∠ABC,
∴∠DBF=∠OBF,
∴∠OFB=∠DBF,
∴OF∥BD,而BD⊥AD,
∴OF⊥AD,即AD与⊙O相切.
(2)解:∵AB=AC,AD是BC边上的高线,
∴BD=CD=
BC=2;∠ABD=∠C;
∴cos∠ABD=cos∠C=
,
∴AB=3BD=6;设⊙O的半径为λ,
则AO=6-λ;
∵OF∥BD,
∴△AOF∽△ABD,
∴
=
,即
=
,
解得:λ=1.5,
∴AE=6-2λ=3.
 (1)证明:如图,连接OF;
(1)证明:如图,连接OF;∵OB=OF,
∴∠OFB=∠OBF,而BF平分∠ABC,
∴∠DBF=∠OBF,
∴∠OFB=∠DBF,
∴OF∥BD,而BD⊥AD,
∴OF⊥AD,即AD与⊙O相切.
(2)解:∵AB=AC,AD是BC边上的高线,
∴BD=CD=
| 1 |
| 2 |
∴cos∠ABD=cos∠C=
| 1 |
| 3 |
∴AB=3BD=6;设⊙O的半径为λ,
则AO=6-λ;
∵OF∥BD,
∴△AOF∽△ABD,
∴
| OF |
| BD |
| AO |
| AB |
| λ |
| 2 |
| 6-λ |
| 6 |
解得:λ=1.5,
∴AE=6-2λ=3.
点评:该题主要考查了圆的切线的判定、相似三角形的判定及其性质等知识点及其应用问题;解题的关键是作辅助线,灵活运用切线的判定、相似三角形的判定及其性质来分析、判断、推理或解答.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
已知B是线段AC上的一点,且BC=
AB,D是AC的中点,若DC=2cm,则AB的长为( )
| 1 |
| 3 |
| A、4cm | ||
| B、3cm | ||
| C、2cm | ||
D、
|
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )| A、(1,4) |
| B、(5,0) |
| C、(6,4) |
| D、(8,3) |

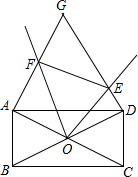 如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.
如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.