题目内容
19．在$\frac{1}{x}$，$\frac{1}{2}$，$\frac{{x}^{2}+1}{2}$，$\frac{3xy}{π}$，$\frac{3}{x+y}$，$\frac{abc}{m}$中，分式的个数是（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．
解答 解：$\frac{1}{x}$是分式，$\frac{1}{2}$不是分式，$\frac{{x}^{2}+1}{2}$不是分式，$\frac{3xy}{π}$不是分式，$\frac{3}{x+y}$是分式，$\frac{abc}{m}$是分式，
故选B
点评 本题主要考查分式的定义，在解答此题时要注意分式是形式定义，只要是分母中含有未知数的式子即为分式．
练习册系列答案
相关题目
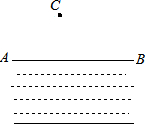如图，是一条河，C是河边AB外一点：现欲用水管从河边AB，将水引到C处，请在图上画出应该如何铺设水管能让路线最短．并说明理由．
如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=8，DH=3，平移距离为4，则阴影部分的面积为26．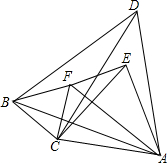
如图所示，平面上三个正三角形ACE，△ABD，△BCF两两共有一个顶点，求证：CD与EF互相平分．