题目内容
3．已知 a2+ab=3，ab+b2=1，试求a2+2ab+b2=4，a2-b2=2．分析 由于a2+2ab+b2=（a2+ab）+（ab+b2），所以将已知两个等式相加即可；由于a2-b2=（a2+ab）-（ab+b2），所以将已知两个等式相加即可．
解答 解：∵a2+ab=3，ab+b2=1，
∴a2+2ab+b2=（a2+ab）+（ab+b2）=3+1=4，
a2-b2=（a2+ab）-（ab+b2）=3-1=2．
故答案为：4，2．
点评 本题考查了整式的加减．解决此类题目的关键是熟练运用合并同类项的法则，这是各地中考的常考点．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
14．下列方程组中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}x=2y+1\\ y=3-z\end{array}\right.$ | B． | $\left\{\begin{array}{l}xy=12\\ x+y=7\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | D． | $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=2\\ 3x-2y=4\end{array}\right.$ |
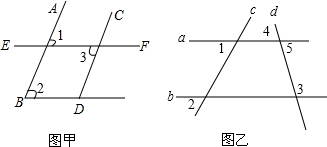（1）如图甲：∠1=∠2=∠3，完成说理过程并注明理由：
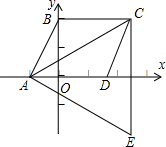如图，已知△ACE是以平行四边形ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称．若点E的坐标是（7，$-3\sqrt{3}$），则点D的坐标是（5，0）．