题目内容
18.用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米.(1)当x为何值时,围成的养鸡场面积为60平方米?
(2)能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.
分析 (1)设围成的矩形一边长为x米,则矩形的邻边长为:32÷2-x,根据矩形的面积的计算方法列出方程求解;
(2)同(1)列出方程,利用根的判别式进行判断方程的根的情况即可.
解答 解:(1)设围成的矩形一边长为x米,则矩形的邻边长为:32÷2-x.依题意得
x2+16x=60,即(x-6)(x-10)=0.
解得 x1=6,x2=10,
即当x是6或10时,围成的养鸡场面积为60平方米;
(2)不能围成面积为70平方米的养鸡场.理由如下:
由(1)知,-x2+16x=70,即x2-16x+70=0
因为△=(-16)2-4×1×70=-24<0,
所以 该方程无解.
即:不能围成面积为70平方米的养鸡场.
点评 本题考查了一元二次方程的应用.解题的关键是熟悉矩形的周长与面积的求法,以及一元二次方程的根的判别式.

练习册系列答案
相关题目
13.设$\sqrt{2}=a,\sqrt{3}=b$,用含a、b的式子表示$\sqrt{0.54}$,下列表示正确的是( )
| A. | $\frac{3ab}{10}$ | B. | 3ab | C. | $\frac{{{a^2}{b^2}}}{10}$ | D. | $\frac{{{a^3}b}}{10}$ |
10.已知等腰三角形的两边分别为3和7,则此三角形的第三边可能是( )
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
7.2cos60°的值等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.不等式组$\left\{\begin{array}{l}{x>-3}\\{x<5}\end{array}\right.$的解集是( )
| A. | x>-3 | B. | x<5 | C. | -3<x<5 | D. | 无解 |
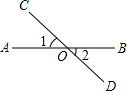 如图,已知点A,O,B在一条直线上,∠1=∠2,你能得到什么结论?试证明你的结论.
如图,已知点A,O,B在一条直线上,∠1=∠2,你能得到什么结论?试证明你的结论. 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)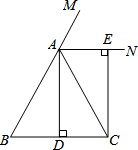 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.