题目内容
17．
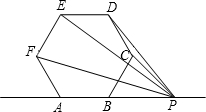如图，正六边形ABCDEF，点P在直线AB上移动，若点P与正六边形六个顶点中的至少两个顶点距离相等，则直线AB上满足条件的点P共有（ ）| A． | 6个 | B． | 5个 | C． | 4个 | D． | 3个 |
分析 先根据正六边形的特点，判断出此六边形中相互平行的边及对角线，再根据线段垂直平分线的性质确定不同的点即可．
解答 
解：如图，分别以一顶点为定点，连接其与另一顶点的连线，在此图形中根据平行线分线段成比例定理可知，CD∥BE∥AF，ED∥FC∥AB，EF∥AD∥BC，EC∥FB，AE∥BD，AC∥FD，
根据垂直平分线的性质及正六边形的性质可知，相互平行的一组线段的垂直平分线相等，在这五组平行线段中，AE、BD与AB垂直，其中垂线必与AB平行，故无交点．
故直线AB上会发出警报的点P有：CD、ED、EF、EC、AC的垂直平分线与直线AB的交点，共五个．
故选：B．
点评 此题主要考查了正多边形和圆，解答此题的关键是找出图中相互平行的线段．
练习册系列答案
相关题目
8．下列计算结果正确的是（ ）
| A． | （-a2）3=a6 | B． | a2+a3=a5 | C． | $\sqrt{4}=±2$ | D． | ${（\sqrt{2}-1）^0}=1$ |
12．
如图：已知点A、B是反比例函数y=$\frac{2}{x}$在第一象限内图象上的两点，AC⊥x轴于点C，BD⊥y轴于点 D，AC与BD相交于点E，设S△ADE=S1，S△EBC=S2，那么（ ）
如图：已知点A、B是反比例函数y=$\frac{2}{x}$在第一象限内图象上的两点，AC⊥x轴于点C，BD⊥y轴于点 D，AC与BD相交于点E，设S△ADE=S1，S△EBC=S2，那么（ ）| A． | S1＞S2 | B． | S1=S2 | ||
| C． | S1＜S2 | D． | S1与S2大小不能比较 |
2．顺次连接正方形各边中点所得的四边形是（ ）
| A． | 等腰梯形 | B． | 正方形 | C． | 菱形 | D． | 矩形 |