题目内容
12. 如图:已知点A、B是反比例函数y=$\frac{2}{x}$在第一象限内图象上的两点,AC⊥x轴于点C,BD⊥y轴于点 D,AC与BD相交于点E,设S△ADE=S1,S△EBC=S2,那么( )
如图:已知点A、B是反比例函数y=$\frac{2}{x}$在第一象限内图象上的两点,AC⊥x轴于点C,BD⊥y轴于点 D,AC与BD相交于点E,设S△ADE=S1,S△EBC=S2,那么( )| A. | S1>S2 | B. | S1=S2 | ||
| C. | S1<S2 | D. | S1与S2大小不能比较 |
分析 先过点A作AF⊥y轴于F,过点B作BG⊥x轴于G,根据反比例函数系数k的几何意义,可得矩形ACOF的面积=矩形BDOG的面积=2,进而得出S1=S2.
解答  解:过点A作AF⊥y轴于F,过点B作BG⊥x轴于G,
解:过点A作AF⊥y轴于F,过点B作BG⊥x轴于G,
∵A、B是反比例函数y=$\frac{2}{x}$上两点,
∴矩形ACOF的面积=矩形BDOG的面积=2,
∴矩形AFDE的面积=矩形BECG的面积,
∵△ADE的面积=矩形AFDE的面积的一半,△BCE的面积=矩形BECG的面积的一半,
∴△ADE的面积=△BCE的面积,
故S1=S2.
故选B.
点评 本题主要考查了反比例函数系数k的几何意义,在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.解决问题的关键是作辅助线构造矩形.

练习册系列答案
相关题目
2. 如图,已知正方形ABCD的边长为4,若BE=5,则CE的长是( )
如图,已知正方形ABCD的边长为4,若BE=5,则CE的长是( )
 如图,已知正方形ABCD的边长为4,若BE=5,则CE的长是( )
如图,已知正方形ABCD的边长为4,若BE=5,则CE的长是( )| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |
4.-1.5的相反数是( )
| A. | 0 | B. | -1.5 | C. | 1.5 | D. | $\frac{2}{3}$ |
 如图,三角形地块中的点B在点A的北偏东35°的方向,点C在点B的北偏西65°的方向,则∠ABC的度数是80°.
如图,三角形地块中的点B在点A的北偏东35°的方向,点C在点B的北偏西65°的方向,则∠ABC的度数是80°.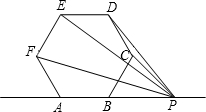 如图,正六边形ABCDEF,点P在直线AB上移动,若点P与正六边形六个顶点中的至少两个顶点距离相等,则直线AB上满足条件的点P共有( )
如图,正六边形ABCDEF,点P在直线AB上移动,若点P与正六边形六个顶点中的至少两个顶点距离相等,则直线AB上满足条件的点P共有( ) 如图,在△ABC中,AC=BC,∠B=70°,分别以点A,C为圆心,大于AC的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接AE,则∠AED的度数是50°.
如图,在△ABC中,AC=BC,∠B=70°,分别以点A,C为圆心,大于AC的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接AE,则∠AED的度数是50°.